UFPE – Cálculo 1 – Listas Prof. Jose Carlos de Albuquerque – Questão 1
Explique a diferença entre um mínimo local e um mínimo absoluto
Passo 1
Oi, tudo bem?
Vamos começar com o que é um máximo ou um mínimo de uma função: quando uma função vai aumentando sua imagem e em um determinado ponto do domínio o valor da imagem estagna e começa a cair: aí temos um máximo da função, como esses pontos circulados aqui embaixo
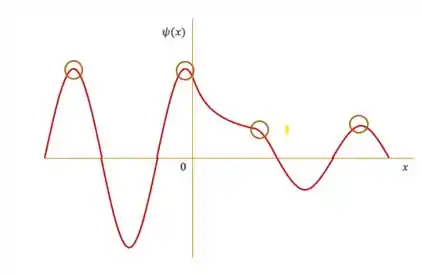
A gente chama esses máximos de máximo local
Isso porque em torno daquela parte da função ela vai apresentar um pico de máximo. Mas será que é o máximo absoluto?
Não sabemos! Máximo absoluto é aquele maior máximo em toda função: é a maior imagem que ela atinge!
Então nesse nosso exemplo o máximo absoluto seria o ponto circulado em azul
Obs.: Podemos olhar pela derivada: derivada passa de valores positivos para negativos – temos um máximo local
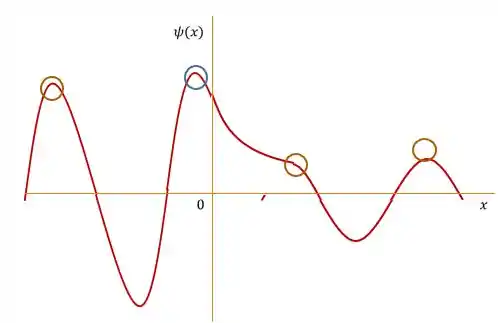
Também teríamos máx absoluto se a função estivesse definida em um intervalo fechado. Dentro de um intervalo fechado sempre teremos máx e mín absolutos: nos pontos críticos ou nos extremos do intervalo
Beleza? Vamos ver o mínimo?
Passo 2
Agora vamos analisar os pontos de mínimo: aqui é o mesmo pensamento, mas com a imagem diminuindo. Em torno do ponto de mínimo local a função vai assumindo cada vez valores menores, até que para essa queda e começa a subir. Nesse ponto temos um mínimo local
Podemos olhar pela derivada: a derivada passa de um valor negativo, para um valor positivo: temos um mínimo local
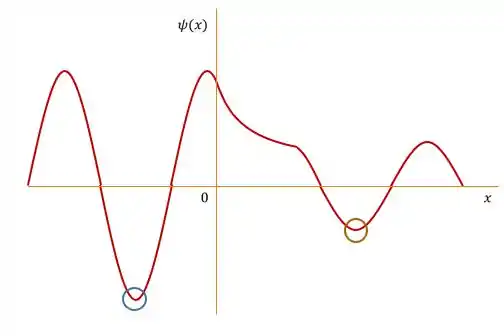
Aparentemente temos um mínimo global no ponto azul: não nessa função não temos um mínimo global! Ué, como assim?
Nota os limites quando dessa função: ela não vai pra nas duas pontas? Vai! Então temos mínimos locais (nos pontos circulados), mas como a função parece que tende a nas duas pontas: não temos um mínimo global!
Teríamos um mínimo global (assim como máximo global) se o intervalo fosse fechado: teríamos obrigatoriamente.
Beleza? Espero ter ajudado!