Explique porque o ponto é um ponto de mínimo da função . O que acontece com a derivada neste ponto?

Bom, um ponto de mínimo de uma função é basicamente o ponto que faz com que a imagem da função seja a menor possível. Como é uma função modular o menor valor que essa função pode assumir é zero. E isso só é possível quando o for igual a zero. Outra maneira de verificar que é um ponto de mínimo é pelo gráfico da função:

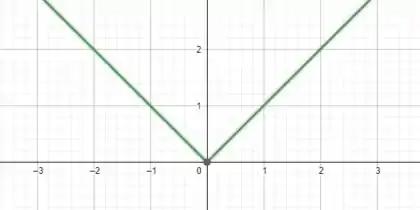
Note que a imagem da função possui um valor mínimo e igual a zero, entretanto não podemos definir uma quantidade para o valor máximo dessa função.

Além disso nos foi questionado qual é a derivada nesse ponto de . E aí qual vai ser esse valor?

Bom, pelo passo anterior já sabemos que esse ponto corresponde ao ponto de mínimo na nossa função , sendo assim podemos afirmar que a derivada nesse ponto NÃO EXISTE. Uma vez que é regra, pontos de máximos e de mínimos não possuem derivada. Outra forma de analisar é pelo gráfico:

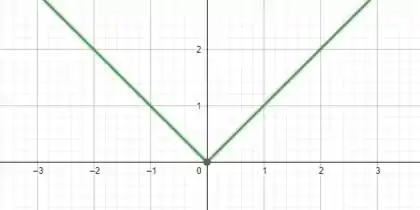
A derivada graficamente representa a inclinação da reta tangente a uma curva. Observe que no ponto a tangente a curva é uma reta paralela ao eixo , dessa forma não havendo inclinação nenhuma em relação a esse eixo. Sendo assim, conclui-se que a derivada nesse ponto não existe.

E aí? Consegui te ajudar? Espero que sim!!!

Bons Estudos!