5) A função possui:
- máximos locais e mínimo local.
- máximo local e mínimo local.
- mínimos locais e máximos locais.
- máximos locais e mínimo local.
Passo 1
Para verificar pontos de máximos ou mínimos, vamos encontrar primeiro os pontos críticos da função , ou seja, pontos que satisfazem ... Derivando então:
Igualando a ...
Então...
ou
Então temos três pontos críticos. Para verificar o que eles são, façamos o estudo de sinal da primeira derivada...
Passo 2
Para o estudo de sinal dela, chamamos e , e analisemos o sinal de cada uma dessas funções...
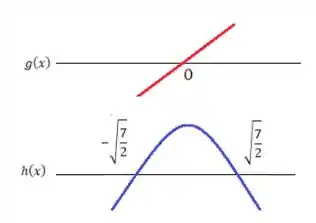
Os produtos desses sinais nos dão o sinal de ...
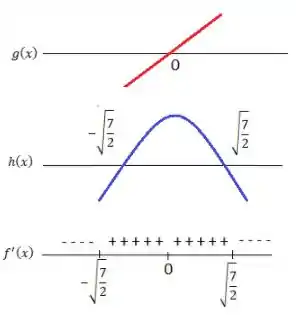
Como de a função é crescente devido ao fato de e de a função é decrescente, o ponto...
Como de a função é crescente, isso faz de um ponto de mínimo...
E de , a função volta a decrescer, fazendo de...
Resposta
- máximos locais e mínimo local.
Exercícios de Livros Relacionados
O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = 3 x 2 - 12 x + 5 ,[ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 x 10 + x 2 - 1
Encontre os números críticos da funçãoh (p) = (p - 1)/(p^2 + 4)