15. Mostre que é um ponto crítico da função , mas não tem um valor extremo local neste ponto.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema, temos que provar que é um ponto crítico da função mas esse ponto não é um ponto extremo.
E aí, tem ideia do que podemos fazer? 🤔
Para obter os pontos críticos de uma função, a derivamos e igualamos a . Assim, os valores para que satisfazem essa igualdade são ditos como pontos críticos.
Depois, para classificarmos um ponto, verificamos se é crescente ou decrescente durante o intervalo ou se muda de comportamento no ponto crítico.
Bora ver como é! 😁
Passo 2
Derivando pelo método de derivação polinomial, temos
Igualando a ...
Por Bhaskara a raiz dessa equação é apenas
Nesse caso, se substituirmos por e por em , vamos obter que
Podemos ver que no intervalo , não assume valores negativos... isso significa que é crescente, fica constante por um momento e volta a crescer. Logo, não é um ponto extremo, é apenas um ponto de inflexão.
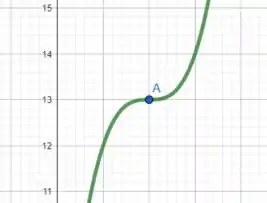
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
é um ponto de inflexão.