Unb - Cálculo 1 - Listas - Lista 8 - Exercício 8
Um ponto é chamado máximo local de se existe tal que
Naturalmente, todo ponto de máximo de é um ponto de máximo local de . Supondo que é um ponto de máximo local de onde a derivada existe, resolva os itens abaixo.
a)Usando a desigualdade acima, verifique que a derivada lateral à direita satisfaz
b) Repetindo o argumento, verifique que a derivada lateral à esquerda satisfaz
c)Lembrando que as derivadas laterais coincidem, conclua que
Passo 1
Olá pessoal lindo do Responde Aí, tudo bem? Essa questão parece complicada, mas vou ajudar você aqui! Vamos começar?
A questão puxa bastante a teoria por isso pode parecer mais complicadinha, mas vamos fazer com calma. Ok?
No item a), devemos verificar se a derivada lateral à direita, ou seja, o tende a pelo lado positivo satisfaz
Vamos supor que hipoteticamente nossa função seja expressa pelo gráfico:
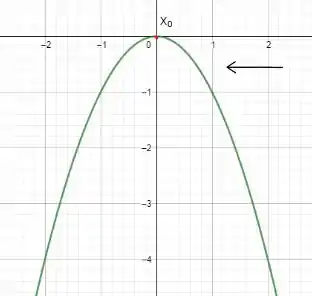
Veja que como o meu sempre estará a direita do meu isso significa que sempre será positivo. Logo, como o enunciado nos informou que para todo significa que
será verdadeiro visto que o numerador da equação sempre será negativo e o denominador sempre será positivo. Portanto pelo jogo de sinal .
Passo 2
Já o item b) quer saber se a derivada lateral à esquerda também satisfaz a
Bom, utilizando o mesmo gráfico anterior porém agora vamos nos aproximar pela esquerda temos que
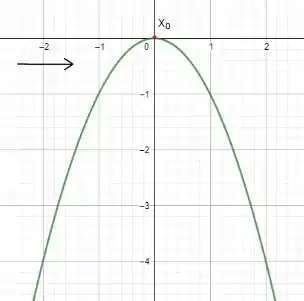
Observe que meu está a esquerda do meu , ou seja, sempre será negativo. Assim
conclui-se que , sempre será positivo. Portanto a derivada também é satisfeita.
Passo 3
Por fim, temos o item c) que deseja que concluirmos o seguinte:
E aí? O que vocês acham?
Bom gente, como os limites laterais coincidem pois a questão afirma isso nesse item, significa que a derivada existe sim nesse ponto. Além disso a questão afirma que é um ponto de máximo local e sabemos que a derivada em pontos de máximos e mínimos locais é , portanto com base em ambos os quesitos podemos afirmar sim que .
E aí? Te ajudei? Show!
Resposta
Resolução nos passos acima