USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 7.28
7.28. Para que pontos da circunferência a soma das distâncias a e é mínima?
Passo 1
Suave na nave?! Tá complicada essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos uma circunferência dada pela equação e queremos descobrir os pontos dessa circunferência que estão mais próximos dos pontos e .
E aí, como fazemos isso? 🤔
A equação da circunferência centrada na origem é dada genericamente como onde é o raio dessa circunferência.
A equação do problema é dada por , ou seja, uma circunferência de raio .
Consegue ver isso? 😁
Passo 2
Esboçando a circunferência e os pontos e , temos
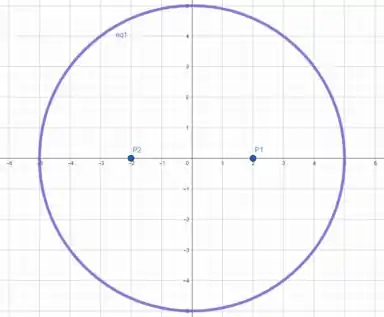
Uma circunferência nada mais é que pontos equidistantes de um ponto no espaço, então se fizermos uma circunferência centrada em , podemos dizer que o ponto mais próximo de a , é o ponto que tangencia a circunferência. E o mesmo podemos aplicar para .
Tranquilo até aqui? 😎
Passo 3
Qual é a menor circunferência que podemos traçar com centro em que tangencie a circunferência ?
Veja só
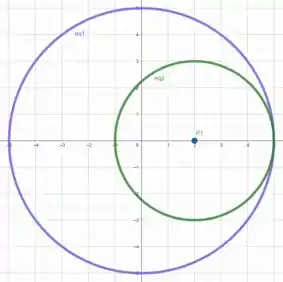
Aqui fica claro que o ponto é o ponto da circunferência que é mais próximo a .
Podemos explicar isso pois uma circunferência tangente a e centrada em intersecta no ponto .
Bacana, não é? 👀
Passo 4
Fazendo o mesmo para ...
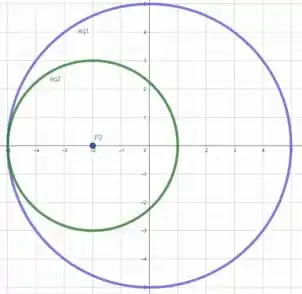
Perceba que o mesmo é valido para , só que no lado oposto, em .
Com isso, vemos que os pontos da circunferencia mais próximos a e são os pontos e
O que achou? Foi de boa? Responde aí! 😊
Resposta
e