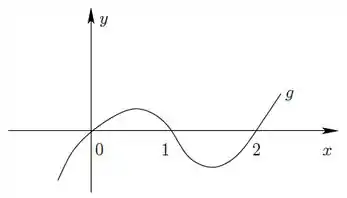
Se é a derivada de uma função , conclui-se que, necessariamente,
- é um número positivo
- possui três pontos de inflexão
- possui um único ponto de máximo local
- possui pelo menos duas raízes reais distintas
Passo 1
O gráfico representa a derivada da função . Por isso, nada podemos afirmar sobres os valores que a função assume nos pontos , e . O que podemos é observar que entre e a função possui um máximo local e entre e ela possui um mínimo local. A função muda de concavidade em apenas um ponto. Portanto, só a alternativa está correta.
Resposta
d. possui um único ponto de máximo local.
Exercícios de Livros Relacionados
O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = 3 x 2 - 12 x + 5 ,[ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 x 10 + x 2 - 1
Encontre os números críticos da funçãoh (p) = (p - 1)/(p^2 + 4)