UFF, Niterói - Praia Vermelha, Cálculo IA, P2 - 2022.2, Questão 4e
Um retângulo deve ser inscrito na elipse . Quais devem ser as dimensões do retângulo, para que sua área seja máxima?
Passo 1
Faaala aí pessoal, tudo bem?
Temos aqui uma questão de otimização. Queremos inscrever um retângulo na elipse:
Lembra que a forma geral da elipse é:
Onde é o centro da elipse.
Comparando com a elipse da questão, concluímos que ela está centrada em , com semieixos valendo e respectivamente.
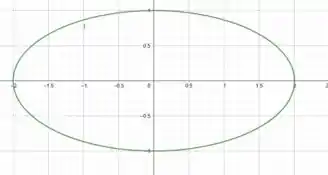
O enunciado nos pede para encontrar as dimensões do retângulo que tornam a sua área máxima.
Para descobrir a área máxima do retângulo que pode ser inscrito nessa elipse, vamos primeiro buscar encontrar uma expressão para a área desse retângulo em função apenas de ou .E, depois derivamos e igualamos a zero, para otimizar a solução.
Bora nessa!!
Passo 2
Vamos imaginar que inscrevemos um retângulo qualquer nessa elipse:
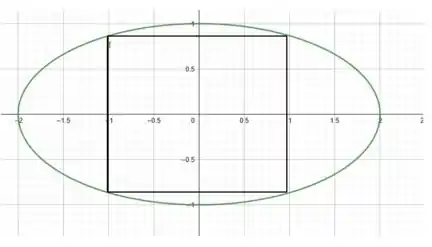
Algo muito importante de perceber é que devido a simetria da elipse qualquer retângulo inscrito nela também será simétrico em relação a origem.
Assim, a área de um retângulo inscrito nessa elipse é dada por:
Onde é a base do retângulo e é a altura.
Mas, da equação da elipse, temos que:
Logo:
Perfeito! Agora que descobrimos a área do retângulo em função apenas de , vamos derivá-la e igualar a zero, para otimizá-la.
Passo 3
Derivando e igualando a zero, encontraremos os pontos de máximo e mínimo dessa função. Estamos interessados em saber o ponto de máximo para obter a área máxima.
Como temos um produto de funções, precisamos usar a regra do produto.
Assim:
Vamos calcular cada uma dessas derivadas separadamente:
Já a derivada do segundo termo é um pouquinho mais complicada. Precisaremos usar a regra da cadeia.
Daí, fazendo:
Temos:
Então:
Já a segunda derivada:
Juntando tudo:
Muito bom!
Assim, vamos ter que:
Logo, temos:
Para que essa expressão seja nula, precisamos ter:
Perfeito! Esse é um ponto de máximo ou mínimo da função. Para verificar que, de fato é um ponto de máximo, podemos olhar para a expressão da derivada de :
Se , temos .
Se , temos .
Ou seja, é um ponto em que a função para de crescer e começa a decrescer. Logo, de fato é um ponto de máximo.
Passo 4
Agora que já obtemos o valor de que dá a área máxima do retângulo, para descobrir a dimensão correspondente basta usarmos que:
Assim:
Portanto:
Ou seja, as dimensões que dão a área máxima do retângulo inscrito na elipse, vale:
É isso aí genteee! Muito obrigado pela atenção, até a próxima 😊