Um retângulo deve ser inscrito em uma semicircunferência de raio . Qual é a maior área que o retângulo pode ter e quais são as suas dimensões?
Passo 1
E aii, galerinha!! Como estão? Vamos juntos pra mais uma!!
Vamos primeiro imaginar a situação que temos, um retângulo será inscrito em uma semicircunferência de raio . E a questão deseja saber qual é a maior área que o retângulo pode ter e quais são as suas dimensões. Temos a seguinte situação:
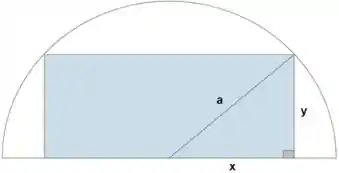
E aí? Como poderemos resolver??
Passo 2
Bom primeiro vamos começar aplicando o teorema de Pitágoras para triângulo retângulo, assim vamos poder relacionar as dimensões do retângulo ao raio da semicircunferência .
E sabemos que a área de um retângulo é dado por:
Como nosso retângulo deve ter área máxima, logo ele deve estar posicionado no meio da semicircunferência, assim a base do retângulo será de acordo com a ilustração do passo anterior. Dessa forma, conclui-se que a área será:
Como ,
, sendo
Passo 3
Como estamos atrás do valor máximo da área do retângulo, vamos derivar a equação da área, uma vez que é no assunto de derivadas que vemos as ideias de máximos e mínimos de uma função.
Aplicando a regra da cadeia temos,
Passo 4
Agora é importante lembrar que quando temos pontos de máximos e mínimos em nossas funções as derivadas nesses pontos são iguais a 0. Portanto para a área ser máxima
Como temos certeza que o , já que . Podemos afirmar que essa equação é igual a zero apenas se o numerador for igual a zero. Logo,
Entretanto . Desse modo só poderá ser .
→ Como então,
Logo,
→ A base do retângulo é
→ E a altura do retângulo é
Passo 5
Agora seus linduxos, temos tudo que precisamos para calcular a área máxima, tendo em vista que já encontramos as dimensões do nosso retângulo. Sendo assim,
E aí? Espero ter te ajudado!
Bora terminar de resolver essa lista para garantir um 10 em cálculo I?!
:)
Resposta
A área máxima é e o retângulo possui de base e de altura.