Seja ABCD um retângulo com diagonal medindo cm. Colamos os lados e para obter um cilindro circular, conforme figura abaixo.
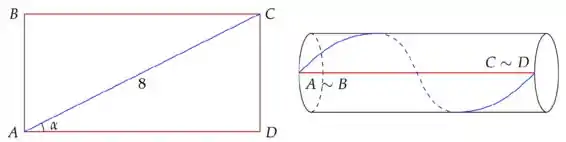
Sendo o ângulo , determine:
1. o volume do cilindro como função exclusivamente de
2. todos os pontos críticos de .
Passo 1
Bom, inicialmente conseguimos perceber que com a medida da seção DC formaremos o perímetro da circonferencia que fica na passe do cilindro, certo? Então temos
Temos ainda que o perímetro da circunferência é dado por
Logo
Passo 2
Bom, o volume do cilíndro nos vai ser dado pela área da base (circunferencia) vezes a altura (Lado AD da folha)
O lado AD nos é dado por
Então voltamos para o volume teremos
Lembrando que já encontrmaos
Passo 3
Tranquilo então, conseguimos especificar o volume em função de
Agora precisamos basicamente encontrr sua derivada e determinarmos quando ela é zero.
Observando essa função percebemos que ela vai zerar onde o seno é zero. Logo,