Seja definida em , cuja derivada tem o seguinte gráfico:
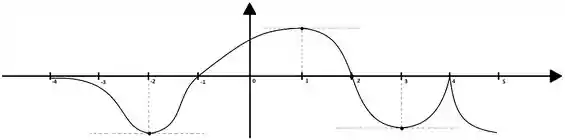
Determine:
(a) Todos os pontos críticos de
(b) Os intervalos onde é crescente e onde é decrescente. Justifique
(c) Todos os pontos de máximo e mínimo local de . Justifique
(d) Todos os pontos de inflexão de . Justifique
Passo 1
(a) Obter todos os pontos críticos de
Antes de mais nada, vamos refrescar a memória: pontos críticos são pontos em que o teste da primeira derivada da 0. Show de bola, então agente só precisa ver quais valores de satisfazem:
Porque serão os valores de em que a inclinação da reta tangente é . Como o gráfico do enunciado é da própria , basta ver as raízes, que vão ser:
Portanto, vão ser pontos críticos:
Passo 2
(b) Obter os intervalos onde é crescente e onde é decrescente, justificando.
Caraca agora complicou. Como eu vou saber isso se não tenho a função ? Relaxa, fica calmo que a gente já tem tudo pra poder descobrir. A derivada não da a inclinação da reta tangente? Então saca só:
Show de bola, agora é só olharmos pro gráfico da e ver os intervalos em que e que . Partiu então:
Passo 3
(c e d) Obter todos os pontos de máximo e mínimo local, além dos pontos de inflexão de , justificando.
Beleza, já sabemos os pontos críticos, não é mesmo? E pontos de máximo e de mínimo são pontos críticos.
Mas pera, então a resposta da letra (a) e da letra (c) são iguais? Não tão rápido meu amigo, da uma olhada aqui:

Temos uma pegadinha! Será mesmo que é um ponto crítico? Vamos testar então. Seja , por exemplo, temos:
Opa, apesar de nesse ponto a inclinação da reta tangente ser nula, em não temos nem pontos de máximo nem pontos de mínimo. O que vai acontecer é que nesse ponto, teremos uma inflexão! A função vai ser decrescente tanto antes quanto depois de mas em mesmo a reta tangente é horizontal. Ficou confuso? Da uma olhada então num gráfico com uma situação semelhante:
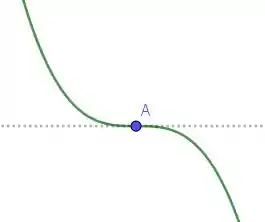
Então sobraram os pontos com e . Partiu então ver quem é de máximo e quem é de mínimo:
E por fim:
Agora, será que esses vã oser os únicos pontos de inflexão? Veja bem, pontos de inflexão são aqueles que fazem:
Oras, então se acharmos uma reta tangente com inclinação nula no gráfico do enunciado, que é de , vamos achar pontos de inflexão! E temos sim três pontos em que isso é verdade:
Agora sim fechamos a questão!
Resposta
(a)
(b)
(c)
(d)