UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 8.34a
Seja
(a) Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo e mínimo.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar os intervalos de crescimento e decrescimento da função, além de determinar seus pontos de máximo e mínimo.
Bom, tanto pra analisar o crescimento/decrescimento da função, quando pra determinar máximos e mínimos, vamos precisar da derivada da função.
Sendo assim, nos pontos onde nossa derivada for nula, temos candidatos a máximo e/ou a mínimo da função, são os chamados pontos críticos. Pra determinar se esses pontos críticos são pontos de máximo ou de mínimo, vamos usar o teste da segunda derivada:
Depois vamos analisar como a função cresce ou decresce fazendo um quadro de sinais e estudando o sinal da primeira derivada da função.
Vamos lá!
Passo 2
Vamos começar calculando a derivada da função . Pra isso vamos usar a regra do quociente na derivação:
Igualando nossa derivada a zero, vamos encontrar os pontos críticos da função:
Então, �� o nosso ponto crítico.
Passo 3
Vamos derivar mais uma vez pra verificar se esse é um ponto de máximo ou mínimo. Derivando , também usando a regra do quociente, temos:
E aplicando o ponto :
Eita, deu zero, e agora? Como a derivada não é maior nem menor do que zero, significa que não podemos afirmar que esse é um ponto de máximo ou mínimo, ele será apenas um ponto de inflexão da função.
Passo 4
Vamos montar nossa tabelinha agora pra estudar o sinal da função. Colocando os pontos críticos em cima e os termos do quociente da derivada separados, juntos com a própria derivada e a função na primeira coluna. Fica assim:
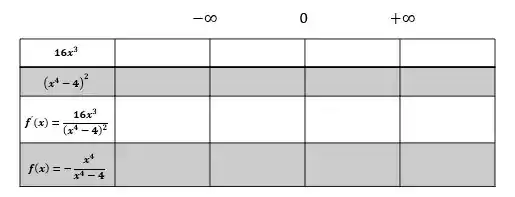
Agora vamos preencher a tabela, começando pela primeira linha, nos intervalos onde a função é negativa e onde ela é positiva. Fazemos a mesma coisa pra segunda linha. Na linha da derivada, multiplicamos os dois sinais que estão acima dela.
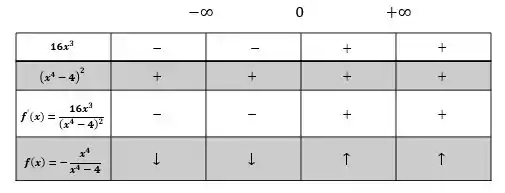
Repare que chegamos ao resultado de que a função está decrescendo no intervalo e crescendo no intervalo , como as setinhas indicam.
Valeu, galera! Até a próxima! 😉