USP– Cálculo 1 – Lista 2 – Questão 1.6b
Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo
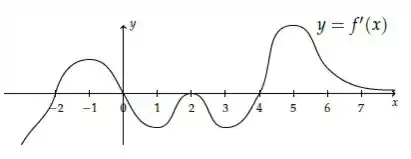
- Para que valores tem um máximo ou mínimo local?
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos dá o gráfico da função derivada de uma função
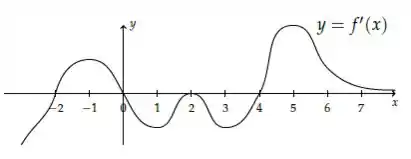
E faz uma pergunta
Para que valores de tem um máximo ou mínimo local?
E agora, como determinar isso?
Sabemos que uma função tem um mínimo local quando a derivada passa de um valor NEGATIVO para POSITIVO, e tem um máximo local quando ela passa de um valor POSITIVO para NEGATIVO
Sendo assim é só a gente olhar pro gráfico da derivada e ver as raízes e o seu entorno!
Beleza?
Bora lá!
Passo 2
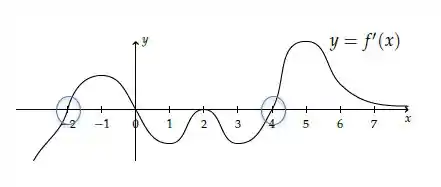Analisando o entorno das raízes temos dois valores em que a função derivada passa de negativo para positivo:
Passo 3
E temos apenas um ponto onde a função derivada troca de sinal de positivo para negativo
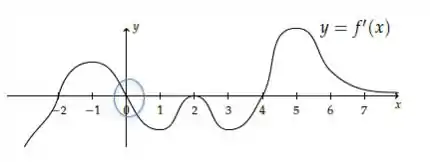
Temos apenas um máximo local:
E é isso! Até a próxima!