UFSCAR – Cálculo 1 – Simulado 3 – Questão 1a
Seja , em que é a função cujo gráfico é ilustrado ao lado
- Em que valores de ocorrem os valores máximos e mínimos locais de ?
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou fazer passo a passo com você! O problema começa dizendo que temos uma função , e que ela é definida em função da integral de outra função
E o que ele nos pede agora na letra (a)? ele pede os valores de nos quais a função apresenta máximos/mínimos locais
Mas onde será que isso acontece? Bom, uma função apresenta máximos e mínimos onde a derivada é igual a zero!
Então nosso primeiro passo é derivar a função para determinar onde a derivada é nula!
Mas e depois? Notou que a função é uma integral? Então aqui vamos usar o teorema fundamental do cálculo para achar a derivada!
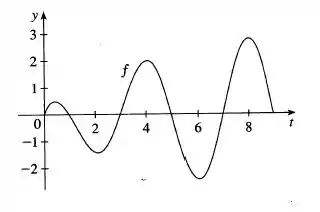
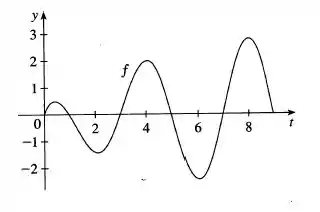
E o que será que tem a ver o gráfico? O gráfico é de , e a derivada de vai aparecer a ! Está aí nossa ligação!
Mas relaxa, vou fazer passo a passo com você! Bora começar?
Passo 2
Nossa função
Derivando temos
E aqui vamos usar o teorema fundamental do cálculo! Como relembrar é viver...
Então vamos aplicar o limite superior em !
Tudo bem até aqui?
E agora? Agora queremos saber onde a derivada é zero! Então o que queremos de verdade é
As raízes de ! E elas nós conseguimos direto do gráfico!
Passo 3
As raízes são os valores de nos quais cruza o eixo ! Vamos rever o gráfico
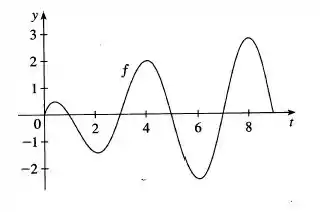
Os pontos nos quais a cruza o eixo são:
Não esqueça de contar o início e o final da função! Nesses pontos a função também toca no eixo !
E é isso! Espero ter ajudado! Até a próxima!