UFSCAR – Cálculo 1 – Simulado 3 – Questão 1b
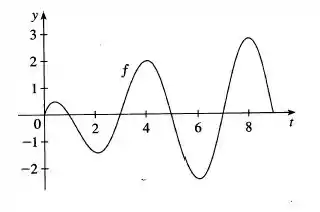
Seja , em que é a função cujo gráfico é ilustrado ao lado
- Em que valor atinge seu valor máximo?
Passo 1
Oi pessoal, tudo certo? Essa questão é uma continuação, então vamos resgatar lá do item (a) o resultado!
O problema nos deu essa função aqui
E através do teorema fundamental do cálculo descobrimos que a derivada de é a :
Então o que temos no gráfico
É o comportamento da derivada de !
Agora nesse segundo item, o problema pergunta em que valor a função atinge seu máximo. Bom, a ideia aqui é pensar em termos de derivada! Pensar onde a derivada representa o máximo de uma função e tentar tirar essa informação do gráfico!
Mas calma, vou fazer com você! Vamos lá?
Passo 2
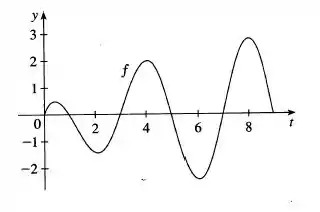
Já sabemos que a derivada de é representada por :
Mas como relacionamos ao valor máximo/mínimo? Pela derivada! A função apresenta um máximo ou mínimo quando sua derivada for igual a zero, ou seja, no nosso caso quando
Tudo bem até aqui?
Esses pontos nós também encontramos lá no item (a): . Mas qual deles representa um máximo e qual deles é maior?
Para isso precisamos lembrar como classificamos como máximo: em torno do ponto crítico, em que a derivada passa de valores positivos para negativos
(os pontos de mínimo são o oposto: a função derivada em torno dele passa de negativa para positiva)
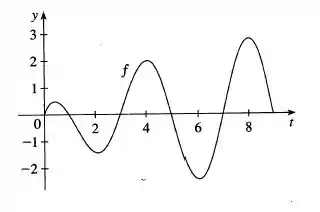Assim, vamos retornar ao gráfico:
Assim os pontos de máximo são em . E de mínimo em
Mas qual dos máximos é o maior? Se nós tivéssemos a cara da função , seria só calcular e e comparas os valores. O maior valor seria o máximo! Mas e agora?
Temos o gráfico da DERIVADA: então vamos olhar para as áreas!
Vemos que os pelo gráfico:
Sabemos que
E
No gráfico fica assim:
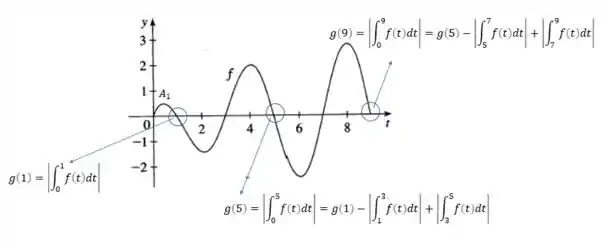
Então, temos que .
Então o máximo absoluto ocorre em . Embora não apareça na nossa classificação de máximos (porque não sabemos o comportamento da derivada para ), pela área podemos afirmar que é um ponto de máximo e mais: máximo absoluto!
Ufa! Terminamos! Bora para o próximo item?