UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.3.1c
Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
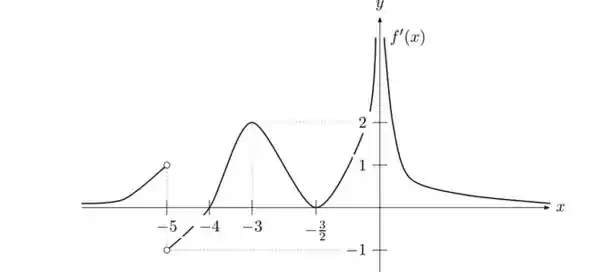
Responda, justificando, o que se pede:
c) Os pontos de máximos e mínimos relativos (locais) caso existam;
Passo 1
Ooi gente, tudo bem?
Nessa questão temos uma função , com a informação de algum dos seus pontos:
Também foi dado o gráfico da derivada de , ou seja,
Além disso, o enunciado também nos falou que:
Nesse item precisamos determinar os pontos de máximos e mínimos relativos.
Vocês lembram o que isso significa?
É justamente onde a função muda a sua direção de crescimento. Ou seja, antes desse ponto ela estava crescendo e após ele, passa a decrescer. E, vice-versa.
Se pensarmos em função da derivada de , é justamente onde se anula, ou seja, troca de sinal.
Vamos analisar o gráfico para encontrar esses pontos.
Passo 2
Temos:
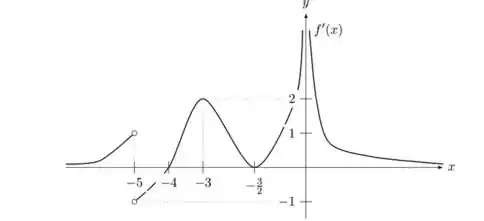
Em:
Tínhamos negativa para e positiva para . Ou seja, a função vinha decrescendo, e em volta a aumentar.
Portanto, esse é um ponto de mínimo relativo!
Em:
Até temos , porém antes desse ponto e depois desse ponto também maior do que . Ou seja, não tivemos um ponto de mínimo ou de máximo.
Sendo assim, o único ponto de máximo ou mínimo relativo é:
É issooo! Obrigado pessoal!
Até a próxima 😊