USP– Cálculo 1 – Lista 2 – Questão 4
Seja . O ponto é ponto de
a. maximo local mas nao global.
b. minimo local mas nao global.
c. maximo global.
d. minimo global.
e. inflexao.
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos dá essa função aqui
E perguntou se o ponto é máximo global, local, se é mínimo global, local, etc.
E agora, como determinar isso?
Quando a derivada primeira é zero podemos ter duas coisas: ponto de máximo ou mínimo. E esse ponto pode ser máximo/mínimo global quando é o maior/menor valor que a função assume, inclusive nos infinitos.
Sendo assim, a ideia é derivar a função dada, igualar a zero e verificar onde a função troca de sinal para achar os pontos de máximo e mínimo. E aí conferir se o está nesses pontos!
Lembrando que se a derivada for zero em um ponto e ela não trocar de sinal significa que esse ponto é de inflexão
Então a ideia é analisar o sinal desse produto com as afirmativas para ver qual delas se encaixa melhor! Beleza?
Bora lá!
Passo 2
A função
Derivando
E agora vamos fatorar aquela parte quadrada dentro dos parênteses! Por soma e produto achamos que as raízes são
Então a forma fatorada é
Beleza?
Passo 3
Temos três pontos críticos
Agora vamos analisar a derivada em torno deles
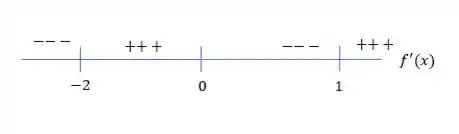
Temos que e são pontos de mínimo. E é ponto de máximo. Mas note que a função é um polinômio de grau par, então ele não tem um máximo global. Assim
é máximo local.
Agora vamos analisar os outros pontos. Em a função vale
E em
A função nos extremos de vai a infinito, então vemos que ele é ponto de mínimo global!
Alternativa correta (d)
E é isso! Até a próxima!