Sejam uma constante positiva e satisfazendo:
a) Determine os pontos críticos, intervalos em que é crescente e intervalos em que é decrescente.
b) Determine e use o teste da derivada segunda para classificar os pontos críticos de .
c) Determine os intervalos em que a concavidade do gráfico de é para cima, os intervalos em que ela é para baixo e os pontos de inflexão do gráfico de .
d) Usando os itens anteriores, faça um esboço do gráfico de supondo que ; ; .
Passo 1
Iae, meus queridos! Tudo certinho?

Temos bastante coisas para resolver nesta questão, mas não se preocupe, vamos chegar no fim sabendo tudo para resolve-la.
No item a) vamos calcular os pontos críticos de , pra isso já temos sua derivada, então igualamos a .
ou
não possui solução, então podemos descartar essa possibilidade.
Portanto é um ponto crítico.
Analisando o gráfico de quando
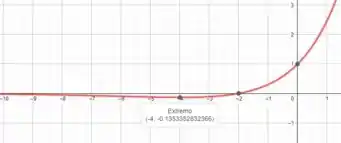
Vemos que a função tende a quando , decresce até quando , cresce a partir desse ponto e atinge o ponto quando .
Com isso, podemos concluir que a função é decrescente até e crescente a partir daí.
Passo 2
No item b) vamos calcular a e classificar os pontos críticos de .
Pela regra do produto, se e
O fator não será importante agora já que é uma constante positiva, então podemos desconsidera-lo.
, logo o ponto em que é um ponto de mínimo.
Passo 3
No item c) analisando o gráfico de novamente, vemos que a função possui uma concavidade voltada para baixo no intervalo de e outra concavidade voltada para cima no intervalo .
Também podemos ver isso igualando a função , seguindo os mesmos passos, vamos encontrar sua raiz como , sabemos que a função decresce quando vem de e cresce a partir de , então nossa afirmação está correta.
No item d) nosso esboço do gráfico será.
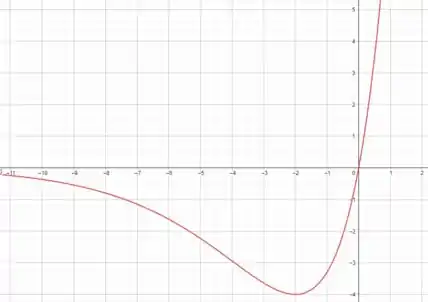
Para facilitar, você pode integrar a função para encontrar uma aproximação de .
É isso! Entendeu tudo? Responde Aí! 😎👍
Resposta
A) Ponto crítico: , , .
B) , logo o ponto em que é um ponto de mínimo.
C) A função possui uma concavidade voltada para baixo no intervalo de e outra concavidade voltada para cima no intervalo .
D) Gráfico no passo-a-passo.