Toda função contínua definida em tem ponto máximo e de mínimo. Use os 3 exercícios anteriores para descrever a estratégia para encontrar os pontos de máximo e de mínimo desta função.

Os pontos de máximos e mínimos em uma função são os chamados valores extremos de ou pontos de inflexão. Bom, os pontos de máximos e mínimos são pontos que normalmente limitam nossa função. Nesse caso, a função pode ter a sua imagem crescendo de determinado ponto ao infinito e/ou a função função pode ter sua imagem diminuindo de um ponto até o menos infinito.

É necessário destacar que existem algumas funções ainda mais limitadas, onde sua imagem sendo valores reais.

Além disso, existe um critério importante que afirma que nos pontos de máximos e de mínimos a derivada da função é igual a zero. Sendo assim, podemos dizer que saber derivar a função nos extremos do domínio é uma estratégia para se encontrar esses pontos de inflexão.

Outra estratégia que podemos utilizar são os gráficos das funções, representar graficamente uma função facilita muito na identificação desses pontos de inflexão. Por exemplo, se

teremos o seguinte gráfico:

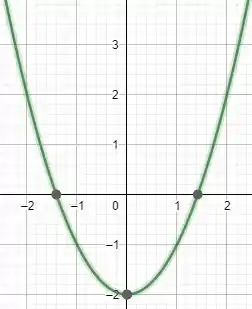
A derivada nada mais é que a inclinação da reta tangente à curva. Então para encontrar esses pontos de máximo e mínimos basta que encontremos os pontos onde a reta tangente não tenha inclinação em relação ao eixo x, ou seja, basta encontrarmos os pontos onde a reta tangente é paralela em relação ao eixo x.

E aí? Essa resolução te ajudou??? Responde Aí!

Bons Estudos!