Lista 2.10 – Derivada de ordem superior – UFSC – Cálculo 1 – Questão C3
Um cabo pendurado entre dois postes toma a forma de uma curva que é o gráfico de uma função que satisfaz a equação diferencial
em que é a densidade linear (massa por unidade de comprimento) do cabo, é a aceleração da gravidade e é a tensão do cabo no ponto mais baixo. Mostre que a função é uma solução da equação diferencial acima.
Passo 1
Falaee, beleza?? Seguinte.. vamos primeiro derivar a função que nos foi dada:
E, fazendo a segunda derivada, temos:
Passo 2
Agora, vamos substituir os valores encontrados em .Se liga aee:
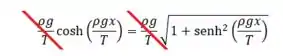
Sabendo que , temos:
Ou seja, a equação diferencial está satisfeita!!
Entendeu direitinho? Responde aee ;)
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Um objeto é lançado para cima com velocidade inicial v 0 metros por segundo a partir de um ponto s 0 metros acima do solo. Mostre que v t 2 = v 0 2 - 19,6 [ s t - s 0 ]
Se uma pedra for atirada verticalmente para cima sobre a superfície da Lua com uma velocidade de 10 m / s , sua altura (em metros) após t segundos será h = 10 t - 0,83 t 2 Qual a velocidade da pedra a
Em que ponto o gráfico da função y = 1 3 x 3 - 3 2 x 2 + 2 x tem tangente horizontal?. Esboçar o gráfico e analisar o resultado obtido.
Derive a função:29 u = t 5 + 4 t 5
Encontre a primeira e a segunda derivadas da função: G r = r + r 3