Considere e funções definidas pelos gráficos abaixo. Sabendo que é tangente ao gráfico da e ao da em , e que corta os eixos nos pontos indicados, faça um esboço, no mesmo par de eixos, do gráfico das derivadas e .
Passo 1
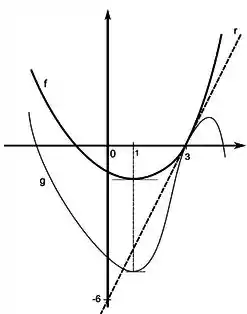
Antes de pensar no gráfico em si da função eu vou tentar achar a equação daquela reta, de onde eu tiro o coeficiente angular e posso dizer que ele será igual às derivadas de e em .
Logo, concluo que o coeficiente angular :
Além disso, ambas derivadas são nulas no , como vemos no desenho que as retas tangentes aos gráficos em são paralelas a .
Passo 2
Vamos concentrar agora na parte onde não temos valores. Sabemos que onde o gráfico cresce a derivada é positiva. Onde decresce ela é negativa. Vou esboçar umas regiões de crescimento e decrescimento para você:
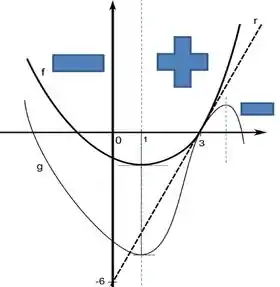
Até as duas derivadas são negativas. A partir daí, positivas. Agora, repara naquele pequeno que eu botei ali no fim, o gráfico volta a decrescer a partir daí, um pouco à frente de . continua crescendo. Agora podemos propriamente esboçar o crescimento e decrescimento:
Passo 3
Agora podemos propriamente esboçar o crescimento e decrescimento das derivadas:
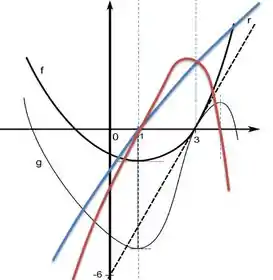
Esclarecendo uma coisa mais: Eu não faço ideia de como é o desenho do gráfico, a única coisa que eu sei é que , e os intervalos de crescimento e decrescimento. O resto vai na criatividade.