Use o gráfico da função para determinar os valores de em que a função é diferenciável e indique os valores de em que a derivada é nula, positiva e negativa.

Um ótimo método de esboçar o gráfico é substituir alguns valores em para encontrar seus valores em e ligar os pontos plotados, por exemplo

Quando , substituir em , quando , substituir em

Plotando esses pontos no plano cartesiano, temos

O próximo passo é ligar os pontos, vemos que é uma equação de com positivo, gerando gráfico de concavidade voltada para cima.

Ao contrário de , que é uma equação de com negativo, gerando um gráfico com concavidade voltada para baixo.

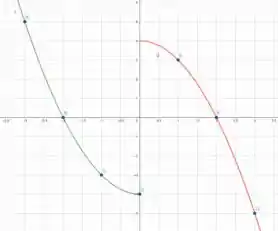
Podemos ver claramente a descontinuidade em , ou seja, nesse ponto a função não é diferenciável.

Com gráfico de , montado podemos calcular as derivadas.

A derivada de uma curva está diretamente relacionada à tangente da mesma, uma derivada positiva consiste em uma reta tangente crescente no ponto calculado, uma derivada negativa consiste em uma reta decrescente no ponto calculado, já uma derivada nula consiste em uma reta tangente constante, ou seja, paralela o eixo

Vamos analisar a curva primeiro quando ,

Derivando , temos

Neste intervalo é negativo portanto qualquer número negativo multiplicado por um número positivo resulta em um número negativo, logo

Porém nesse caso quando a derivada não pode ser calculada já que os limites laterais nesse ponto são diferentes, logo em a função não é diferenciável.

Analisando o gráfico quando ,

Derivando

O mesmo acontece nesse caso, como é sempre positivo e está sendo multiplicado por um número negativo, a derivada da função quando será sempre negativa.

Com isso chegamos à conclusão de que, com exceção de , a derivada de é negativa e em a função não é diferenciável.

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍