Sendo a função dada pelo gráfico abaixo, diga onde a derivada de é positiva, negativa ou nula.
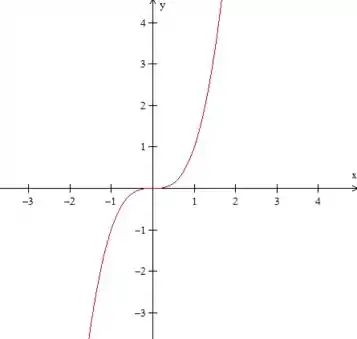
Passo 1
Basicamente o enunciado está nos pedindo o sinal da derivada de .
Bom... Caso você tenha se esquecido, a derivada de em um determinado ponto nada mais é do que o coeficiente angular da reta tangente à curva naquele ponto.
Com isso, nós temos que analisar alguns pontos distintos desse gráfico para identificarmos se esse coeficiente é positivo, negativo ou nulo.
Mas antes, se liga nesses exemplos:
a)
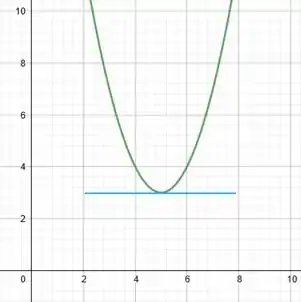
A reta tangente à curva não possui inclinação.
b)
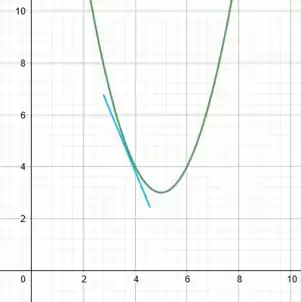
A reta tangente à curva é decrescente.
c)
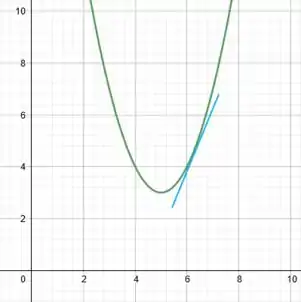
A reta tangente à curva é crescente.
Passo 2
Graficamente, se nós analisarmos a derivada de para valores à esquerda de , conseguimos identificar que o coeficiente é positivo, certo?
Dá uma olhadinha aqui:
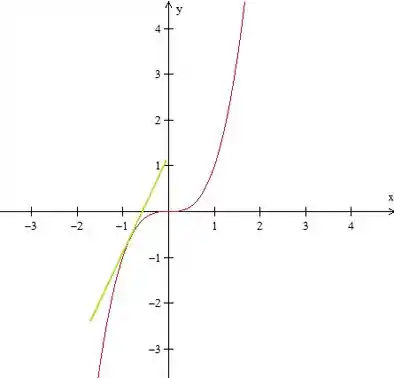
Como a reta verde (reta tangente à quando ) é crescente, o seu coeficiente angular é positivo.
Com isso, temos que: quando , .
Passo 3
Mais à direita do gráfico, em uma outra análise, o coeficiente angular da reta tangente à também é positivo:
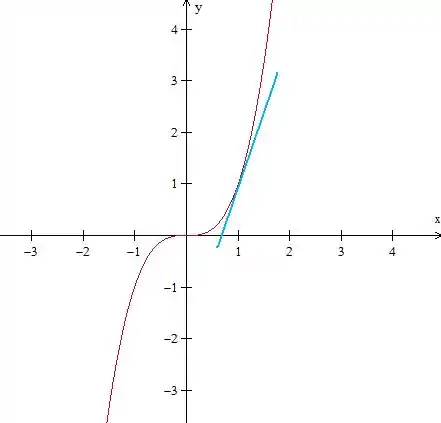
Isso acontece, pois a reta azul (reta tangente à quando ) é crescente.
Com isso, temos que: quando , .
Passo 4
Agora vamos analisar o ponto central, quando :
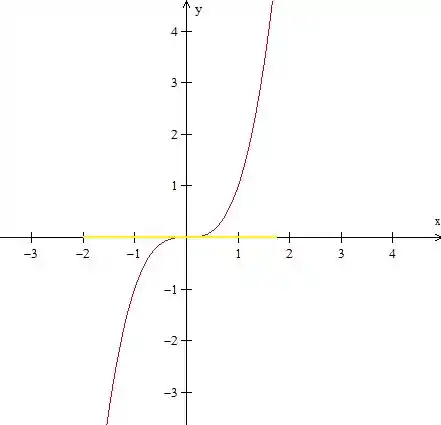
Como podemos ver, nesse ponto, a reta amarela (reta tangente à quando ) não possui inclinação, logo, é nula.
Com isso, temos que: quando , .
Resposta
Portanto, temos que quando: