UFABC – Cálculo 1 – Lista 1 – 2
Mostre que não existe a derivada de em . Calcule a derivada para
Passo 1
E aí, galerinhaaa! Pra essa questão a gente vai precisar lembrar do que é o módulo!
O resultado do módulo é sempre o que está dentro do módulo com sinal positivo e negativo, ou seja, se temos , o resultado disso é -x ou x
Passo 2
Se aplicarmos a derivada então nos resultados que saem do módulo, nós temos:
Note que isso nos dá algo mais ou menos assim graficamente:
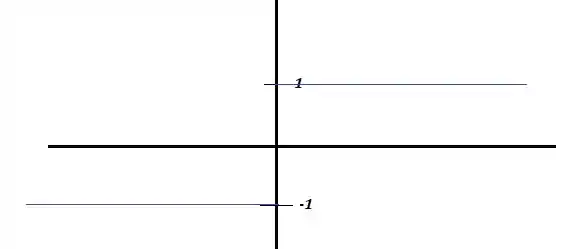
A gente tem um salto ali em , ou seja, tem uma descontinuidade em zero, e por isso, não existe a derivada em . E pelo próprio gráfico vemos que não importa qual valor diferente de zero o assuma, sempre teremos o seu valor em ou . Quando , teremos o valor de -1, quando , teremos o valor de 1
Resposta
Demonstração
Exercícios de Livros Relacionados
Um objeto é lançado para cima com velocidade inicial v 0 metros por segundo a partir de um ponto s 0 metros acima do solo. Mostre que v t 2 = v 0 2 - 19,6 [ s t - s 0 ]
Se uma pedra for atirada verticalmente para cima sobre a superfície da Lua com uma velocidade de 10 m / s , sua altura (em metros) após t segundos será h = 10 t - 0,83 t 2 Qual a velocidade da pedra a
Em que ponto o gráfico da função y = 1 3 x 3 - 3 2 x 2 + 2 x tem tangente horizontal?. Esboçar o gráfico e analisar o resultado obtido.
Derive a função:29 u = t 5 + 4 t 5
Encontre a primeira e a segunda derivadas da função: G r = r + r 3