UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 11.4
Jane está em um barco a 2 km da costa e deseja chegar a uma cidade litorânea localizada 6 km
ao longo de uma linha costeira retilínea desde o ponto (na costa) mais próximo do barco. Ela
rema a 2 km/h e caminha a 5 km/h. Onde ela deve aportar para chegar à cidade no menor
tempo possível?
Passo 1
Eaew, belezinha?
A questão pede para a gente calcular onde Jane deve aportar para chegar o mais rápido possível na cidade destino. Vamos dar uma olhada na situação:
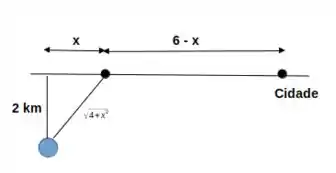
O tempo total que Jane irá gastar para chegar até a cidade é dado por
Onde , , , são as distâncias e as velocidades em água e em terra, respectivamente. Da figura, utilizando o teorema de Pitágoras e supondo que Jane aporte no ponto x, temos que a distância percorrida por água é dada por e por terra
Então, o tempo total gasto por Jane para chegar até a cidade é de
Agora podemos determinar a distância x em que Jane deve aportar para gastar o menor tempo possível, derivando a função tempo total e igualando-a a zero, já que em um ponto de extremo de uma função, a sua derivada é nula. Então vamos lá derivar!
Passo 2
Como a derivada de uma soma de funções é a soma das derivadas, precisamos derivar cada termo da expressão. Utilizando a regra da cadeia para o primeiro termo, obtemos
Igualando a expressão acima a zero, obtemos
Elevando os dois lados da equação ao quadrado, achamos
Checando os pontos de limites do intervalo para o qual a função tempo total está definida (), nos certificamos de que o valor encontrado, de fato, representa a distância que minimiza o tempo, pois
Então, para que Jane chegue à cidade no menor tempo possível, ela deveria aportar à m do ponto de menor distância.
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
À metros do ponto de menor distância.