Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra de L’Hospital – Indeterminação ∞/∞ e 0/0

Ver Teoria
Exercício 531234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515254555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule os seguintes limites

(b) lim x → 0 + ⁡ x x

Passo 1

Lembrar de propriedades do logarítimo

Opa, pera. Logarítimo? Porque vamos precisar disso se a função é x x ? Bem, da uma olhada:

lim x → 0 + ⁡ e f x = e l i m x → 0 + f x

Ok ok, mas quem é esse f x ai? Bem, se:

ln ⁡ e f x = f x ln ⁡ e =   f x

Então:

ln ⁡ e ln ⁡ f x = ln ⁡ f x ln ⁡ e = ln ⁡ f x

E logo:

e ln ⁡ f x = f x

Em outras palavras, se:

f x = x x

Vamos finalmente ter

e ln ⁡ x x = x x

Rearranjando então o limite original:

lim x → 0 + ⁡ x x = lim x → 0 + ⁡ e ln ⁡ x x = e l i m x → 0 + ln ⁡ x x

Vamos então calcular o limite la de cima agora e achar nossa resposta

Passo 2

Calcular o limite em cima de e

O limite que ficou em cima de e foi:

l i m x → 0 + ln ⁡ x x

Esse malandro ai vai precisar ser reescrito também. Vamos ajeitar ele para que possamos usar L’Hospital:

l i m x → 0 + ln ⁡ x x = l i m x → 0 + x ln ⁡ x = l i m x → 0 + ln ⁡ x 1 x  

Derivando em cima e em baixo:

l i m x → 0 + ln ⁡ x x = l i m x → 0 + 1 x - 1 x 2 = l i m x → 0 + - x = 0

Passo 3

Juntar os resultados

Finito! Agora é só juntarmos os resultados. Vimos que:

lim x → 0 + ⁡ x x =   e l i m x → 0 + ln ⁡ x x

l i m x → 0 + ln ⁡ x x = 0

Então vamos ter:

lim x → 0 + ⁡ x x = e 0 = 1

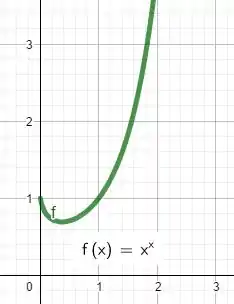
Graficamente, vemos que esse resultado se aplica:

Resposta

lim x → 0 + ⁡ x x = 1

Exercícios de Livros Relacionados

Encontre o limite. Use a Regra de L’Hospital onde for apropriado. Se existir um método mais elementar, use-o. Se a regra de L’Hospital não for aplicável, explique por quê. lim θ → π / 2⁡ 1 - s e n ( θ
Determinar os seguintes limites com auxílio das regras de L’Hospital. lim x → 0 ⁡ cosh ⁡ x - 1 1 - cos ⁡ x
Use Lh’ospital o limite underset(x - 0)(lim) (t g x)/(x + s e n x)
Calculel) underset(x - 0)(lim) (t g 3 x - s e n x)/(s e n^3 x)
Encontre o limite.underset(x - 0)(lim) (t g x)/(x)