UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - 1ª Lista - 2022.2, Questão 12
Q12. Considere , com uma função duas vezes diferenciável. Então, a função é duas vezes diferenciável e satisfaz.
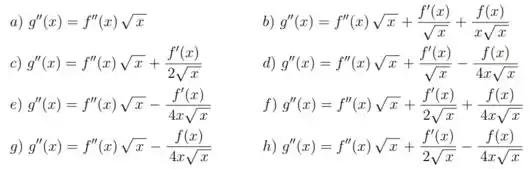
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema foi dada a função e nosso objetivo é calcular a segunda derivada de .
Lembra como fazemos isso? 🤔
No caso, é o produto das funções e e portanto, para calcular a derivada de , temos que aplicar a regra do produto.
A regra do produto é calculada a partir da formulinha
Sacou? Bora começar! 😉
Passo 2
Calculando a primeira derivada de a partir da regra do produto, temos
Derivando novamente pelo mesmo método temos...
Comparando com as alternativas do problema, temos que a alternativa correta é dada por
É isso! Essa resolução te ajudou? Responde Aí! ✌
