UnB, Sem Campus, Cálculo 1, P3 - 2014.2, Questão 2
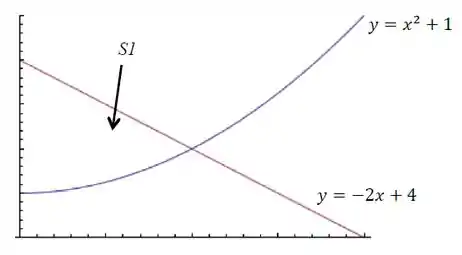
Com base na figura abaixo, determine a área da região , delimitada por , e ; e determine o volume do sólido gerado pela revolução de em torno do eixo .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra gente encontrar a área da região que é mostrada na figura e, em seguida, determinar o volume do sólido de revolução que é gerado na rotação dessa região. Mas vamos por partes!
Pra determinar a área da região, a gente vai precisar olhar pra figura e ver que a função tá acima da função , naquela região . E aí a gente pode usar a fórmula da área entre curvas pra calcular:
Onde e . O enunciado também diz que a região tá delimitada em , só não diz até onde. Mas repare que ela vai até o ponto de interseção das curvas, que acontece quando . A partir daí nós vamos definir nossos intervalos de integração.
Por fim, pra calcular o volume do sólido de revolução, nós vamos usar a equação:
Vamos lá!
Passo 2
Pra gente encontrar, vamos começar encontrando nossos limites de integração fazendo:
Vamos achar as raízes dessa equação, usando Bhaskara:
Mas repara que a nossa região tá somente na parte positiva do eixo :
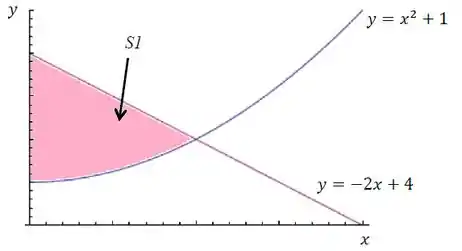
Então, vamos escolher o . Substituindo em qualquer uma das funções nós obtemos:
Portanto, a nossa interseção tá no ponto . E a nossa região vai de até .
Passo 3
Agora podemos calcular nossa área:
Substituindo , e o intervalo do passo anterior, temos:
Integrando cada termo:
Aplicando os intervalos de integração em :
Passo 4
Agora só falta a gente determinar o volume do sólido gerado pela revolução de em torno do eixo . Pra isso, nós vamos usar a equação:
Substituindo e , temos:
Abrindo esses produtos:
Integrando cada termo:
Agora só falta aplicar os limites de integração:
Prontinho, galera! Até a próxima! 😉