Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas em torno de
Passo 1
Opa galera, aqui nós temos uma questão bem característica de cálculo diferencial e integral. Para ser mais especifico é a parte de integral. Aqui a questão pergunta qual é o valor do volume do solido de revolução formado pela intersecção das curvas girando em algum eixo de simetria.
Você deve ter ficado, que diabos é isso?

Vamos devagarzinho, para começar precisamos desenhar os gráficos. Em Questões envolvendo integrais, se você desenhar algo errado tem uma tendencia muito grande de apresentar algum erro na resolução, belezinha?
Ai tu deve se perguntar, além de cálculo preciso saber desenho?

Calminha, Calminha. Existem diversos softwares que servem para isso, mas na sua prova vai precisar então precisamos praticar.

Deeeeeeeixa disso, fica tranquilo, vamos resolver juntinhos ok?
Vamos desenhar passo a passo e depois resolver essa integral para que você possa entender o assunto 1000%.
Passo 2
Primeiramente vamos desenhar a função mais complicadinha que é a primeiramente devemos perceber que quando ela tende para números muito grandes negativos o tende a crescer, porém quando ela tende para números muito grandes positivos ela tende a diminuir e quando o o .
Sendo assim, o gráfico dela deve ficar algo mais ou menos assim:
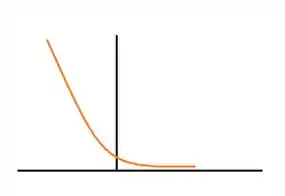
Agora vamos inserir os pontos mais simples que é as retas e
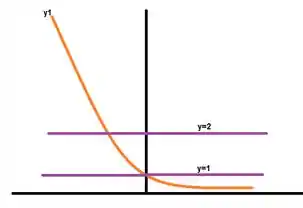
Agora precisamos finalizar o nosso gráfico com apenas a reta . Que finalmente concluímos essa etapa com a seguinte figura.
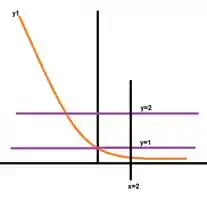
Viu como desenha? É bem legalzinho né? Bem, mas aí vem a pergunta: o que vamos fazer agora?
Vamos encontrar a região delimitada por todas as curvas e depois girar em torno da função .
A região delimitada se você olhar direitinho é essa aqui que pintamos de vermelho:
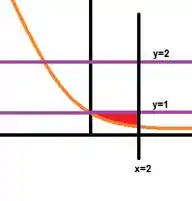
E girando em torno do eixo temos a seguinte figurinha:
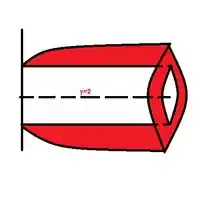
Passo 3
Agora que enxergamos a figura que é gerada após a revolução vamos para o que importa, a resolução da integral.
Analisando as figuras nós vemos que o nosso intervalo de integração vai do ponto até o ponto pois, é nesse ponto que é a intersecção das retas deixando o nosso dominiozinho fechadinho e bonitinho.
A segunda etapa é saber as funções que limitam nossa figura superiormente e inferiormente.
Analisando a seguinte figura podemos enxergar melhor isso:
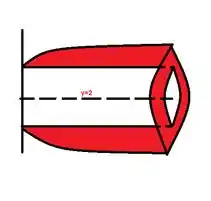
Aqui podemos analisar e enxergar que a camada externa do cilindro é coberta pela função exponencial e internamente é pela função constante .
Porém devemos nos concentrar em um detalhe, em relação ao eixo elas estão transladadas e precisamos corrigir isso, logo:
E consequentemente
Passo 4
Utilizando a expressão para o cálculo de um volume de revolução temos a seguinte formulinha:
Desenvolvendo os quadrados temos a seguinte expressão:
Aplicando os limites de integração temos que: