Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 351234567891011121314151617181920212223242526272829303132333436373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere a região R delimitada pelas retas 3 y - 2 x + 1 = 0 , y = x , y = 1 e y = 3 .

  1. Esboce a região R .
  2. Escreva uma integral, ou uma soma de integras, que represente(m) o volume do sólido de revolução obtido pela rotação da região R ao redor da reta y = 4 .
  3. Calcule o volume.

Passo 1

Vamos começar esboçando a reta como a questão pede. Vamos ver a primeira:

3 y - 2 x + 1 = 0

Isolando y , temos: 3 y - 2 x + 1 = 0 ⟹ 3 y = 2 x - 1 ⟹ y = 1 3 2 x - 1

Opa! Vamos ver quando toca os eixos agora para podermos traçar. Corta o eixo x quando y = 0 : 0 = 1 3 2 x - 1 ⟹ 2 x - 1 = 0 ⟹ x = 1 2

Corta o eixo y quando x = 0 : y = 1 3 - 1 = - 1 3

Ou seja, a reta passa pelos pontos: 1 2 , 0 0 , - 1 3

Ficando:

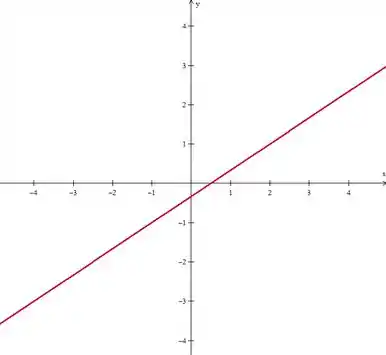
Para a outra reta, temos simplesmente y = x que passa pela origem e segue com inclinação 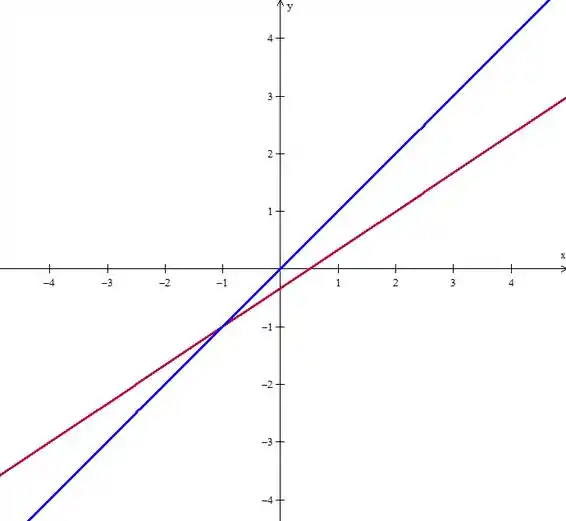1 :

Finalmente, restam y = 1 e y = 3 que são constantes:

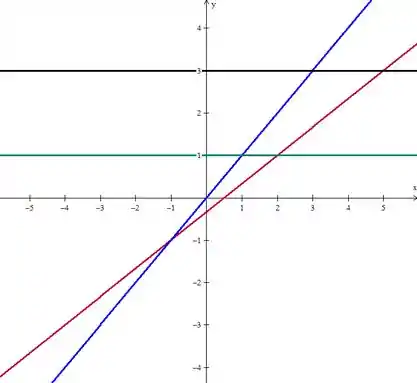
A nossa região R vai ser aquela que está entre todas as retas:

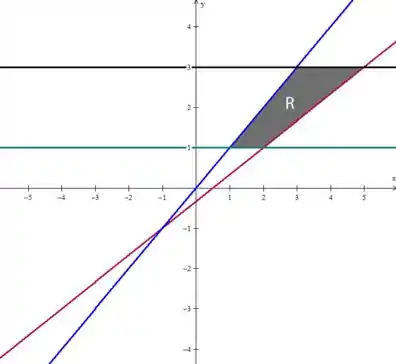
Passo 2

Agora precisamos escrever as integrais que determinam o volume de revolução dessa região em torno da reta y = 4 .

V f = π ∫ a b f m a x x - 4 2 - f m i n x - 4 2 d x

Para tal, precisamos dividir a região em diferentes regiões com uma curva superior e outra inferior cada, para que possamos substituir os valos de f m a x e f m i n .

Dessa forma, separamos R , em R 1 , R 2 e R 3 , ficando:

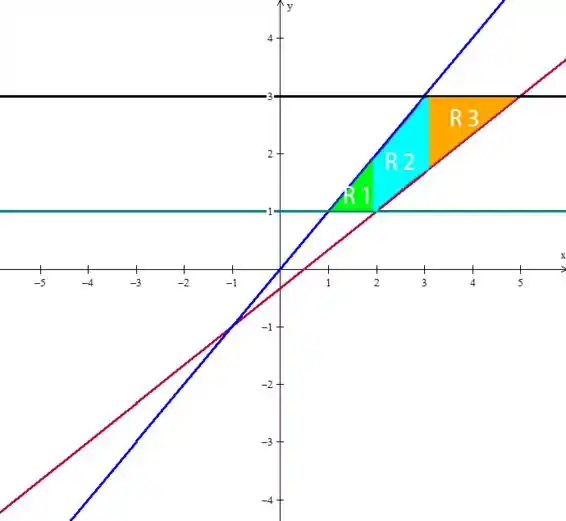
Veja que R 1 começa em x = 1 e termina em x = 2 . A curva inferior a reta y = x (mais próxima de y = 4 ), a curva superior é y = 1 . Ficando: V R 1 = π ∫ 1 2 1 - 4 2 - x - 4 2 d x = π ∫ 1 2 9 - x 2 - 8 x + 16 d x = π ∫ 1 2 - x 2 + 8 x - 7 d x  

Agora temos R 2 , começando em x = 2 e indo até x = 3 . Tendo curva inferior y = x e superior y = 2 x - 1 / 3 :

V R 2 = π ∫ 2 3 2 x - 1 3   - 4 2 - x - 4 2 d x = π ∫ 2 3 2 x 3 - 13 3 2 - x - 4 2 d x

= π ∫ 2 3 4 x 2 - 52 x + 169 9 - x 2 - 8 x + 16 d x

= π 9 ∫ 2 3 - 5 x 2 + 20 x + 25 d x

Finalmente, R 3 , começando em x = 3 e indo até x = 5 . A curva inferior é y = 3 e a superior é y = 2 x - 1 / 3 :

V R 3 = π ∫ 3 5 2 x - 1 3 - 3 - 4 2 2 - 1 d x = π ∫ 2 3 2 x 3 - 13 3 2 - 1 d x

= π ∫ 2 3 4 x 2 - 52 x + 169 9 - 1 d x

= π 9 ∫ 3 5 4 x 2 - 52 x + 160 d x

O volume de revolução de R será a soma do volume de revolução de região:

V R = V R 1 + V R 2 + V R 3

V R = π ∫ 1 2 - x 2 + 8 x - 7 d x + π 9 ∫ 2 3 - 5 x 2 - 4 x - 145 d x + π 9 ∫ 3 5 4 x 2 - 52 x + 160 d x

Passo 3

Agora, precisamos calcular essas integrais para determinar o volume. Temos integrais de polinômios, então não será complicado determina-las:

∫ 1 2 - x 2 + 8 x - 7 d x = - x 3 3 1 2 + 4 x 2 1 2 - 7 x 1 2 = - 8 3 + 1 3 + 4 ⋅ 4 - 4 + - 7 ⋅ 2 + 7 =

- 7 3 + 12 - 7 = - 7 3 + 5 = 15 - 7 3 = 8 3

1 9 ∫ 2 3 - 5 x 2 + 20 x + 25 d x = 1 9 - 5 3 x 3 2 3 + 10 x 2 2 3 + 25 x 2 3

= 1 9 - 95 3 + 50 + 25 = 130 27

1 9 ∫ 3 5 4 x 2 - 52 x + 160 d x = 1 9 4 3 x 3 3 5 - 26 x 2 3 5 + 160 x 3 5

= 1 9 392 3 - 416 + 320 = 104 27

Logo, teremos:

V R = 8 3 π + 130 27 π + 104 27 π = 72 + 130 + 104 27 π = 34 π 3 u . v .

Sem esquecer do u . v . que indica unidade de volume.

Resposta

V R = 34 π 3 u . v .

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .