Seja a região limitada pela curva e pelas retas e . Determine o volume do sólido de revolução gerado pela rotação de em torno, do eixo
Passo 1
Primeiro eu preciso desenhar a região:
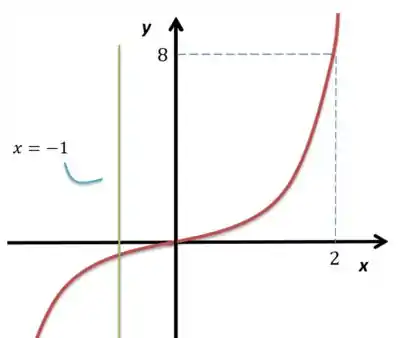
Repara que a área que eu estou trabalhando é essa entre o vermelho, o pontilhado do nível e o eixo . Bom, como vou integrar em , preciso da minha função em :
Agora integro no formato da integral para seções transversais. Repara só em uma coisa, minha função raio será a própria função , já que o eixo de rotação dista do eixo :
E aí, acabou? Não, é essencial que você não esqueça que entre o eixo e o de rotação fica um vácuo que você precisa levar em conta. Ele vai gerar um cilindro de raio e altura , ou seja:
O volume total da figura, então, é:
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .