Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 102123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFRJ – Cálculo 1 - Listas do AVA - lista 17 – Questão 6

Um objeto é esculpido a partir de um tronco cilíndrico de madeira maciça com diâmetro de 2 L metros e comprimento de 4 metros. O objeto tem a forma do sólido de revolução obtido pela rotação, em torno do eixo x , da região limitada pela curva y = L 2 x 2 + x , x ∈ 1,5 e pelo eixo x . Calcule o volume de madeira desperdiçado.

Passo 1

Faaalaa, belezinha?? Bora para mais um probleminha dessa lista.

Para entender o que tá rolando, bora fazer um desenho do que está acontecendo:

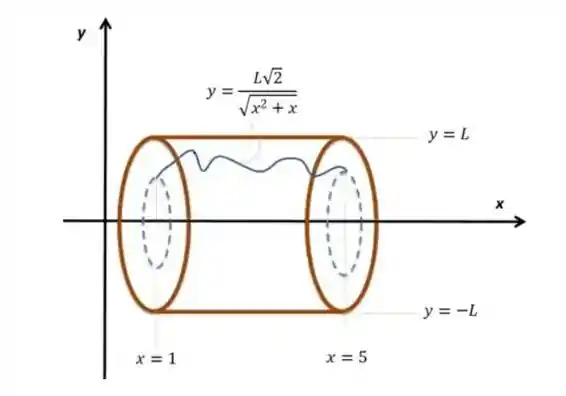
Nesse desenho a linha azul passa a ideia da função que será rotacionada. Não cabe muito a nós entendermos muito bem como ela é, basta sabermos que é sempre positiva, pois é um numero positivo sobre uma raiz, além de ser continua no intervalo estudado.

Com isso, conseguimos falar quem é o volume desperdiçado, consegue entender o motivo?

Veja que o volume desperdiçado será o volume total do tronco (cilíndrico) menos o volume rotacionado dessa funçãozinha aí.

Vamos lembrar, que o volume do cilindro é dado por:

V = π r 2 h

Pela figura, conseguimos substituir os valores, tendo:

V = π L 2 5 - 1 = 4 L π

Passo 2

Agora, para achar o outro volume, bora aplicar a seguinte formula:

V =   ∫ a b π f x 2 d x

Substituindo os parâmetros do problema:

V = ∫ 1 5 π L 2 x 2 + x 2 d x  

Elevando ao quadrado e jogando constantes para fora, temos:

V = 2 L 2 π ∫ 1 5 1 x 2 + x d x  

Aqui, temos algo que aparece bastante, vamos usar que:

1 x 2 + x = 1 x x + 1

=   1 x - 1 x + 1

Ou seja:

V =   2 L 2 π ∫ 1 5 1 x - 1 x + 1 d x

Por isso, temos:

V = 2 L 2 π ln ⁡ x - l n ⁡ ( x + 1 ) 1 5  

Usando que a subtração de log���s é o quociente do que está dentro, temos:

V = 2 L 2 π ln ⁡ x x + 1 1 5

Substituindo:

V =   2 L 2 π ln ⁡ 5 6 - ln ⁡ 1 2

Usando a mesma propriedade:

V =   2 L 2 π ln ⁡ 5 6 1 2  

Ou seja, chegamos que:

V = 2 L 2 π ln ⁡ 5 3

Passo 3

Porém, vamos lembrar que queremos o volume geral menos esse, ou seja:

V d e s p e r d i ç a d o = 4 π L 2 - 2 L 2 π ln ⁡ 5 3

Ajustando um pouco:

V d e s p e r d i ç a d o = 2 π L 2 2 - ln ⁡ 5 3  

E assim chegamos ao fim de mais uma questãozinha dessa lista, bora para a próxima?

Resposta

2 π L 2 2 - ln ⁡ 5 3  

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .