Utilize o método das seções transversais para determinar o volume do sólido gerado pela rotação da região limitada por:
em torno do eixo .
Passo 1
Oi galerinha, tudo bom?
Nessa questão temos uma região no plano delimitada pelas curvas:
Precisamos determinar o volume do sólido gerado ao se rotacionar essa região em torno do eixo . Além disso, devemos fazê-lo usando o método das seções transversais.
Como a rotação é em torno do eixo , vamos tomar esse eixo no nosso método das seções, e aí aplicamos:
onde é a área da seção transversal do sólido. Já e estão relacionados ao intervalo que delimita a região no .
Tranquilo?
Passo 2
Bom, vamos começar esboçando a região plana que será rotacionada:
Bom, vamos começar esboçando a região plana que será rotacionada:
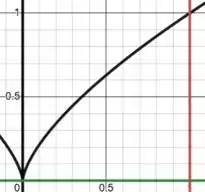
A curva preta é justamente a reta:
Que limita a nossa região inferiormente (vamos rotacionar em relação ao eixo ).
Já a reta vermelha é a reta:
Que limita a região superiormente.
Assim, a área da seção transversal rotacionada em torno do eixo , vale:
Daí, substituindo na integral:
Muito bom!
Passo 3
Agora, vamos resolver a integral:
Logo:
Prontinho gente, obrigado pela atenção 😊