UFCG. Cálculo Diferencial e Integral II. Listas de Cálculo 2 UAMat. Lista 3. Questão 3d.
3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
(d) , , , .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema, temos que obter o volume do solido que é gerado ao rotacionar a região limitada pelas curvas , , e , ao redor do eixo .
Primeiro temos que analisar como é dado a região que vamos revolucionar!
Plotando as curvas e hachurando a área entre elas, temos
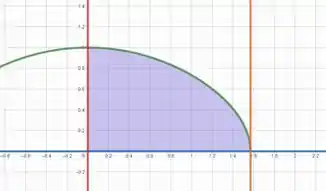
Consegue imaginar como será o sólido ao rotacionar essa área ao redor do eixo ? Seria algo parecido com uma bola oval cortada ao meio 👀
E como podemos calcular o volume desse sólido? 🤔
Pra isso, podemos usar o método dos discos, sabe como funciona? 😁
Passo 2
Esse método consiste em dividir o sólido em infinitos discos de alturas infinitesimais, como se fatiássemos o sólido perpendicularmente ao eixo .
O volume de um disco é dado por
Onde é o raio do disco e é a altura.
Podemos dizer que o raio do disco é dado pela distância de até , ou seja, , já é uma altura infinitesimal que vamos chamar de .
Fazendo essas substituições na equação, temos que cada volume infinitesimal será dado por
Integrando os dois lados, temos
Estamos interessados apenas na região que está entre e , então aplicamos esses valores nos limites de integração de
Tranquilo até aqui? 👀
Passo 3
Como é uma constante, podemos tirá-la para fora da integral
Pelo teorema fundamental do cálculo, a integral de é dada por . Não podemos calcular a integral de pelos métodos convencionais, então apelamos para o teorema.
Aplicando os limites de integração...
Substituindo em , temos
Portanto, o volume do solido formado pela revolução da área que tínhamos obtido é dada por ! Legal, né? 😁
Fim! Iae, o que achou? Responde Aí! 😁
