Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 861234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848587888990919293949596979899100

Enunciado

UFCG - Sem Campus - Cálculo Diferencial e Integral II- Listas - Teste 9 - Lista 3 - Questão 5 - Alternativa a)

Determine o volume dos sólidos obtidos com a rotação, em torno do eixo x , da região limitada pelas curvas:

a ) y = x ,   y = 1 ,   x = 0

Passo 1

Opa! Tudo bem com você?

O enunciado quer que calculemos o volume do sólido de revolução da região delimitada por

y = x ,   y   =   1 ,   x = 0

em que a rotação é realizada em torno do eixo x . Temos que a região é o triângulo mais escuro dado a seguir.

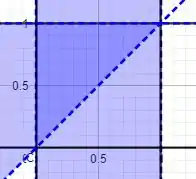
Que após rotacionada em torno do eixo x forma o seguinte sólido

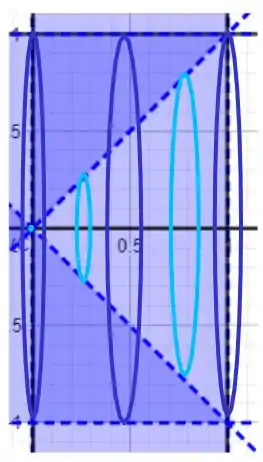
É um cilindro em que você cavou um cone! Consegue visualizar? Mas como calculamos o volume disso? Quanto temos sólidos com um buraco no meio temos que considerar este volume que falta em nossos cálculos! Mas como fazer isso? Calculamos o volume como um todo, em nosso caso um cilindro de raio f ( x ) = 1 , portanto

V c i l i n d r o   =   ∫ a b π [ 1 ] 2 d x = π ∫ a b d x

e, então, desconsideramos o buraco! Que tem um “volume” calculado pelo método de discos, considerando um disco com raio dado por f ( x ) = x , ou seja

V b u r a c o   =   ∫ a b π [ x ] 2 d x = π ∫ a b x 2 d x

E, portanto, o nosso volume é simplesmente

V = V c i l i n d r o - V b u r a c o = π ∫ a b [ 1 - x 2 ] d x

Essa fórmula pode aparecer com outros formatos, mas quando estamos rotacionando em torno do eixo x este formato serve! Os limites a e b , indicam onde o sólido começa e termina no eixo x . Vamos tentar resolver? Vem comigo!

Passo 2

Usando a nossa função x = f ( y ) , com os limites indo de a = 0 até b = 3 . Portanto, temos que

V   =   π ∫ 0 1 [ 1 - x 2 ] d x

Podemos dividir isso em duas integrais da forma

V   =   π ∫ 0 1 d x - π ∫ 0 1 x 2 d x

Ambas as integrais podem ser resolvidas através da seguinte regrinha

∫ a b x n d x = 1 n + 1 x n + 1 | a b = 1 n + 1 [ b n + 1 - a n + 1 ]

para n = 0 temos que

∫ 0 1 d x = x | 0 1 = [ 1 - 0 ] = 1

e, para n = 2 , temos que

∫ 0 1 x 2 d x = 1 2 + 1 x 2 + 1 | 0 1 = 1 3 [ 1 3 - 0 3 ] = 1 3

Portanto, juntando estes resultados, temos que o nosso volume é

V   =   π ( 1 ) - π ( 1 3 ) = 2 3 π

A questão foi isso! te vejo na próxima! Tchauzinho!

Resposta

V   = 2 3 π

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .