Questão 3: Seja
- Esboce a região do plano compreendida pelo gráfico de e o .
- Encontre o volume do sólido obtido pela revolução de em torno do eixo .
(Use uma integral imprópria adequada!)
Passo 1
Para desenhar essa função , vamos começar desenhando a primeira parte da função que é
Essa função tem a cara de uma parábola...
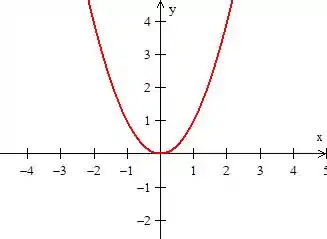
Epa! Mas a função delimita essa parábola em e ...
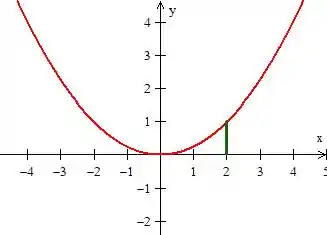
Quando então , percebeu?
Passo 2
Agora desenhamos a segunda parte da função...
O desenho dessa função é semelhante ao de ...
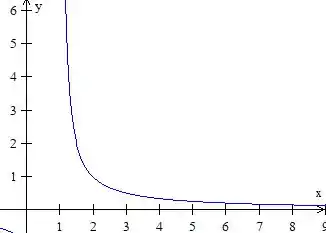
Só que essa hipérbole está desloda inteiramente para direita de uma unidade pois sacou? Do mesmo jeito que anteriormente a função delimita a curva em pra lá.
Perceba que aqui também , então quando colocarmos essas duas partes do gráfico de em um único plano, vamos obter...
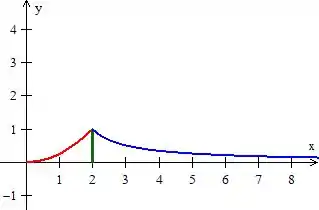
Esse é justamente o gráfico de ;D
Passo 3
Mas você vai me questionar: “uai, mas não é isso que a gente quer no item do problema. Queremos a região que vai da função até o eixo ”.
E você está commpllletamente certo! Essa região é essa daqui oh...
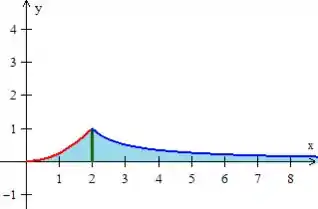
Prontinho ;)
Passo 4
Quando giramos essa região ao redor do eixo vamos obter um sólido de revolução só que no infinito, saca? O problema nos pede o volume dele. Ora, se ele tem volume, então a integral que vamos calcular que tem os limites lá no infinito (uma integral de volume imprópria) vai convergir.
Mas que integral é essa? Ora! Para o cálculo de um volume de uma região que gira em torno de é melhor calcularmos pelos métodos dos discos...
Onde e são os limites do sólido em , ou seja, é onde começa, no , e onde “termina”, no infinito positivo nesse caso...
Bem, mas repare que a função tem definições diferentes...
Então de até , consideremos uma função de até o infinito outra. O volume total vai ser a soma das duas...
Bora calcular essas duas integrais?
Passo 5
Vamos começar com a mais fácil aqui...
Integrando esse polinômio...
Passo 6
Quanto à outra... A imprópria...
Essa integral é pela definição, é um limite...
A integral
Podemos calcular:
Substituindo os limites de integração...
Passo 7
Aplicando o limite no resultado da integral...
Ora, por propriedades de limites...
O primeiro limite é uma constante e quando vai ao infinito ele não se altera, portanto...
Já esse outro...
Logo...
Passo 8
Como vimos o volume é a soma das duas integrais que calculamos...
Resposta
a)
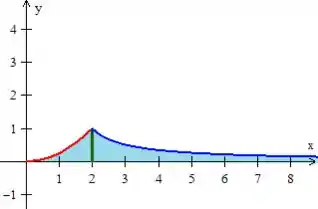
b)