UFCG; Cálculo 2; Lista-3; questão 14 d.
Calcule o volume do sólido obtido com a rotação da região triangular limitada pelas retas , e , em torno:
d) da reta , usando o método do anel.
Passo 1
Saaalve galerinha, animam destruir essa questão comigo?
O enunciado nos diz que há uma região criada pelo limite das seguintes retas:
, ,
Podemos plotar o gráfico e perceber a região amarela foi formada. Olha só!
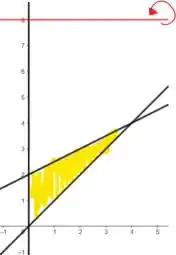
A dúvida é: quando essa região rotacionar ao redor da reta , qual vai ser o volume do sólido? Vem descobri comigooo!
Passo 2
A ideia aqui é usar o método do anel que tem o objetivo de calcular o volume de um sólido com um buraco no meio. Assim como pode ser visto na imagem abaixo, o volume é a diferença entre o volume da região maior e o volume da região menor.
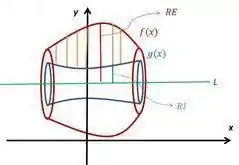
Portanto precisamos saber o raio externo e o raio interno . Como o sólido rotacional ao redor da reta , então:
Nesse caso, o volume do sólido de revolução obtido pela revolução da região R em torno da reta é dado por:
Passo 3
Substituindo na fórmula, temos:
Simplificando a equação.
Prontinho, encontramos o volume do sólido! Curtiu a resolução? Responde Aí ;)