Calcular o volume da região delimitada pelas equações , , em torno da reta . Considere = raio interno e =raio externo.
No cálculo do volume foi obtido um e e um volume superior a
No cálculo do volume foi obtido um e e um volume superior a
No cálculo do volume foi obtido um e e um volume inferior a
No cálculo do volume foi obtido um e e um volume inferior a
Passo 1
Oiiie, tudo bem?
O enunciado nos indica as informações necessárias para calcular o volume de um sólido de revolução, em torno de uma reta constante vertical , e cuja região rotacionada é delimitada pelas curvas e . Vamos primeiro visualizar esta região, ela é a seguinte
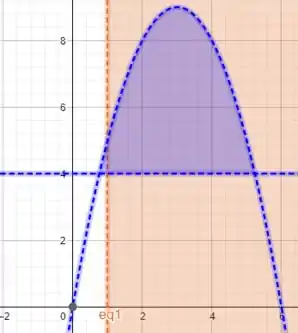
Precisamos rotacionar esta região em torno de . E então obteremos uma região similar a seguinte
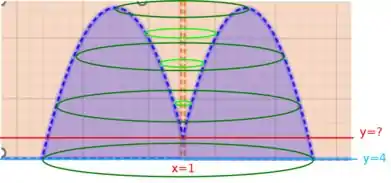
Se fizermos fatias horizontais de espessura podemos obter coroas infinitesimais, cujo o volume é dado pela área de sua base vezes a sua espessura. A área da base de uma coroa circular, no entanto é . E o volume será a soma de todos estes infinitesimais
Vamos calcular agora o nosso volume!
Passo 2
O primeiro cuidado que devemos ter é relacionado ao raio interno, note que indiquei na figura acima uma reta com , eu indiquei esta região pois ela indica o momento em que o raio interno muda de valor! Então por facilidade vou calcular o volume de meu sólido até esta região e somar com a volume da região superior mais tarde. Belezinha? Nesta região temos que o sistema é simplesmente um disco com raio dado pela própria função como
Aplicando Bhaskara, temos
Temos que o nosso raio externo será o valor . Ainda precisamos de saber o limite superior, precisamos saber qual é o valor máximo de nossa função, isso pode ser obtido pelos métodos de cálculo. Saca só!
Passo 3
O máximo de uma função é obtido quando temos um ponto crítico, ou seja, e temos que . Vamos ver se encontramos o valor de , temos que
Que é zero quando , portanto, . A segunda derivada é tal que , sempre negativa, portanto, necessariamente é o máximo! O valor de é
Que é simplesmente . Beleza, temos tudo que precisávamos para resolver nossa integral! Vamos escrevê-la!
Passo 4
Temos nosso volume como
Vamos resolver esta integral! Vem comigo!
Passo 5
A primeira coisa aqui é expandir aquele quadrado, temos
Juntando as constantes, e, separando as integrais temos
A primeira e a terceira integral acima podem ser resolvidas identificando suas primitivas. Para a segunda vamos trabalha-la um pouquinho antes! Chega junto!
Passo 6
Vamos considerar a integral
Para enxergar mais facilmente o resultado, vamos fazer uma substituição simples , e, portanto,
Que pode ser identificada como
Avaliando os limites de integração, temos que
Vamos identificar as integrais que faltam agora!
Passo 7
Temos na equação (2) a integral
E, também a integral
Ou seja, substituindo ambos estes resultados e a equação na equação, temos
Vou deixá-la assim, pois queremos um valor numérico no final, e não tem porquê ficar mexendo com as frações, certo? Bora calcular o resto do volume que falta!
Passo 8
No entanto, considera partes que não deveria, e devemos desconsiderar uma parte. Devemos construir um novo volume em que o raio interno tem outro valor, que já obtivemos quando fizemos Bhaskara anteriormente, como tínhamos considerado o valor positivo para o lado mais exterior, o lado mais interior tem que estar relacionado ao sinal negativo, certo? Portanto o raio interno agora é
O limite inferior de integração é , indicado pela reta vermelha em minha imagem no Passo 1, é possível obter avaliando a função em . Vamos escrever a nossa integral!
Passo 9
Para a parte superior do sólido, temos
Vamos expandir estes quadrados
Assim como fizemos anteriormente, vamos juntar as constantes e separar as integrais
Nós já resolvemos estas integrais antes, mas com limites diferentes! Dá uma olhada lá em cima! No próximo passo vou escrever o resultado mais diretamente, belezinha?
Passo 10
Temos
E o nosso volume toma a forma
Agora só precisamos somar os dois volumes! E temos o nosso resultado! Uff...
Passo 11
O volume total do sólido é
Que pode ser escrito como
Resultado que vou jogar na calculadora para obter
Ou seja, nenhuma alternativa é verdadeira!