Q01V) Responda às perguntas abaixo no espaço adequado no seu caderno de respostas. As soluções devem ser sucintas e a resposta final deve estar destacada do restante da solução.
- A integral representa o volume de um sólido de resvolução. Descreva o sólido
Passo 1
Outra questãozinha de sólido de revolução. Essa pode enrolar um pouco a cabeça, mas saca só, o método dos discos tem essa cara:
Ok, mas como isso ajuda? Bem, ta vendo que tem um multiplicando um termo ao quadrado? Vamos tentar mexer na integral do enunciado até isso aparecer:
Temos duas opções agora que dão duas respostas diferentes, então vamos separar em passos diferentes. A primeira opção é aplicar a distributiva de e a segunda é aplicar a distributiva só de .
Passo 2
Vamo que vamo, aplicando a distributiva então de , ficamos com:
Ta vendo que ta cheio de termos ao quadrado do lado do ? É exatamente isso que queríamos! Ajeitando um pouquinho mais, chegamos em:
Isso nada mais é do que do que o volume de um cilindro substraido de um cone duplo. Primeiro olha pro cilindro, ele vai ser a revolução da região retangular abaixo abaixo:
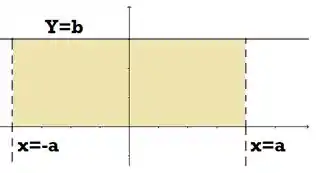
O cone duplo é formado pela revolução em torno do eixo de dois triângulos. A outra integral representa então o volume da seguinte região rotacionada:
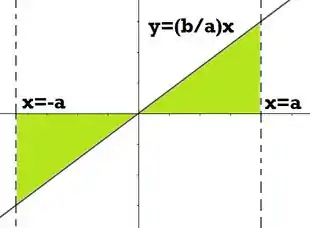
Se quisermos desenhar a região que vamos rotacionar, já que o volume maior é o do cilindro e ele está desenhado em , podemos usar uma forma análoga da região do cone duplo:
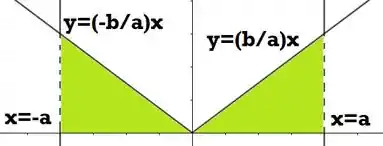
O retângulo bege menos essa nova área verde desenhada nos dá a nossa região :
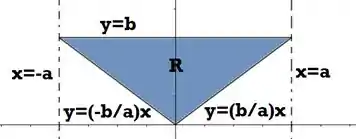
Sólido gerado pela rotação da região limitada pelas curvas , e em torno do eixo .
Passo 3
Agora bora aplicar a distributiva de , ficando com:
Ok, mas e daí? Bem, pensa o seguinte. Se:
Então caímos exatamente num modelo de método dos discos, mas quem é essa função ai? Bem, vamos dar uma mexida nessa função. Pra começar, vamos elevar ao quadrado os dois lados:
Opa, peraí, uma equação de curva de elipse? Isso mesmo! A última equação nada mais é do que a equação de uma elipse com semieixos e , centrada na origem! Só que como uma elipse não é uma função, na hora de isolarmos o , chegamos a:
O que separa a elipse em parte de cima e de baixo, respectivamente as parcelas positiva e negativa. Bem, não importa qual você insira no método dos discos, como ele vai elevar ao quadrado de novo, o resultado vai ser o mesmo. Mas pra responder uma coisa só, vamos considerar que a região é:
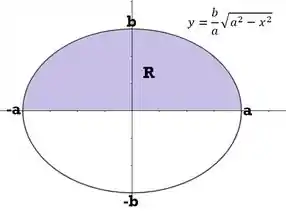
O sólido é gerado pela rotação em torno do eixo da parte superior de uma elipse de semi-eixos e . Este sólido é chamado elipsóide
Resposta
Existem duas respostas possíveis:
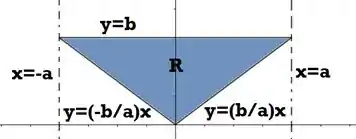
Sólido gerado pela rotação da região limitada pelas curvas , e em torno do eixo .
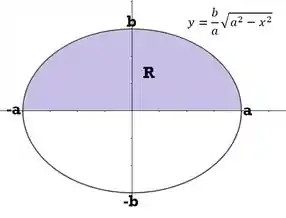
O sólido é gerado pela rotação em torno do eixo da parte superior de uma elipse de semi-eixos e . Este sólido é chamado elipsóide