UFMG – Cálculo 1 – P3 – Questão 5
Divida uma pizza circular de de diâmetro através de cortes paralelos de maneira que cada uma das três partes tenha a mesma área
Passo 1
Oi, tudo bem? Essa questão parece inocente, mas quanto mais você pensa, mais ela fica estranha!
Mas relaxa, vou fazê-la passo a passo com você! Bora lá! Temos uma pizza circular de diâmetro , ou seja, de raio
Beleza? E queremos dividir em três partes iguais: isto é, de forma que cada pedaço tenha da área total da pizza
E esse aqui é o pulo do gato!
Uma vez que a gente sabe quanto deve ser a área de cada fatia, a ideia é associar essa área com uma integral definida
Assim vamos poder encontrar o ponto de em que essa divisão exata acontece!
Mas calma! Vou fazer passo a passo com você!
Passo 2
Vamos começar fazendo um esboço da região da pizza! Podemos inserir um sistema de coordenadas que coincida com o centro da pizza.
Vamos fazer dois cortes paralelos de tal forma que a área total da pizza fique divida exatamente em partes iguais.
Tranquilo até aqui?
O raio do círculo é , e ele estará centrado na origem, então
Mas ainda não sabemos em que ponto (que deve estar entre ) devemos colocar as nossas retas paralelas a fim de que seja separado exatamente em três. Então vou chamar esse ponto de .
Assim podemos relacionar essas áreas com uma integral definida, dá uma olhada no esboço
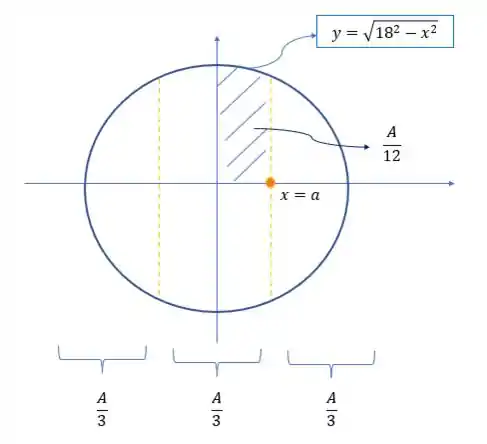
Note que se pegarmos a faixa central, vemos que ela pode ainda ser dividida em partes (por conta dos eixos cartesianos e porque garantimos que o círculo está centrado na origem), assim a área hachurada é
Mas quanto vale a área total? Sabemos o raio da pizza, logo sabemos a área total!
Assim a área hachurada deve valer
Tudo bem até aqui?
Passo 3
Mas o que isso tudo tem a ver com a integral definida? Tem a ver que sabemos qual é a função que representa essa área! Sabemos também os limites
E sabemos o quanto essa integral deve dar
Combinando tudo isso podemos resolver a integral, aplicar os limites, e determinar qual é o valor de , ou seja, determinar onde cortar a pizza!
agora vamos montar nossa integral!
E agora? Agora é #partiu resolver a integral!
Bora trabalhar nisso?
Passo 4
Precisamos resolver essa integral aqui
Como temos vamos usar substituição trigonométrica!
E os limites? Quando :
Agora quando :
Substituindo temos
Simplificando por dos dois lados da igualdade temos
Aqui usamos a identidade trigonométrica
E agora é só integrar!
Beleza? E agora aplicar os limites de integração
Simplificando o que for possível
E ficamos com essa coisa linda! É isso! Temos uma equação transcendental e deixamos indicado assim mesmo!
Ufa! Terminamos! Então a resposta é
Espero ter ajudado! Até próxima!