Cálculo de Volume através de Integrais
Seja a região limitada pelos eixos e pelo arco de parábola , para entre e .
c) Calcule o volume do sólido obtido girando a região acima em torno da reta
Passo 1
Vamos começar vendo como fica o gráfico dessa função, temos uma parábola com o coeficiente de negativo. Além disso, as raízes vão ser
A parábola vai ser
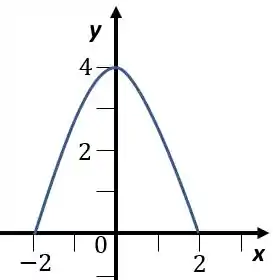
Mas ele só quer de à , então vamos ter
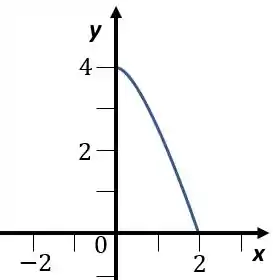
Passo 2
Como temos uma função de , e estamos rotacionando em uma reta paralela ao eixo vamos usar o método das cascas cilíndricas. Precisamos achar o raio e a altura da casca, vamos olhar de novo a figura da rotação para nos ajudar
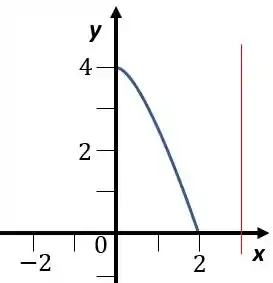
O raio vai ser a distância de à , porque é a distância da reta que estamos rodando até a função.
A altura vai ser a própria função
O volume vai ser
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .