Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 671234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666869707172737475767778798081828384858687888990919293949596979899100

Enunciado

3. Sera R a região limitada pela curva y = ln ⁡ x e pelas retas x = 0 , y = 1 e y = 2 . Faça um esboço de R e calcule o volume gerado pela rotação de R em torno do eixo y .

Passo 1

Oi, galerinha! Tudo bom? Aqui o que problema nos da dois comandos: calcular o volume e esboçar a região.

Então vamos começar desenhando a região, identificando nela os limites de integração e depois integrando para achar o volume.

Bora lá!

Passo 2

A região que o problema descreve é limitada por y = ln ⁡ x e pelas retas x = 0 , y = 1 e y = 2 . Então vamos encontrar essas interceções com y = ln ⁡ x

Então vamos desenhar a região:

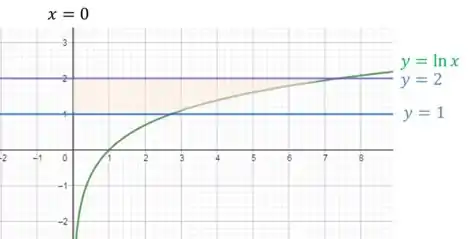
Agora vamos montar a nossa integral!

Passo 3

Para calcular o volume da região que acabamos de encontrar ao rotacionarmos no eixo y , vamos seguir a seguinte relação:

V = π ∫ a b g y 2 d y

No eixo x , ela está sendo limitada entre os pontos x = 0 e x = e y (que é a função inversa da função y = ln ⁡ x ).

Já no eixo y , ela está sendo limitada entre as equações y = 1 e y = 2 .

Sendo assim, a nossa integral ficará,

V = π ∫ 1 2 e y - 0 2 d y = π ∫ 1 2 e 2 y d y

Vamos agora encontrar a nosso volume!

Passo 4

Integrando,

V = π ∫ 1 2 e 2 y d y

Ficamos com,

V = π ∫ 1 2 e 2 y d y = π 1 2 e 2 y | 2 1

V = π e 4 - e 2 2

Resposta

V = π e 4 - e 2 2

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .