a) Considere os parboloides
e
Determine a equação da projeção no plano da curva interseção dos paraboloides. Esboce também esta projeção.
b) Calcule o volume da região espacial
c) Encontre a posição do centroide da região indicada no item 1b.
Passo 1
a) Para achar a projeção em da curva de interseção entre esses dois paraboloides, a gente substitui o valor de de uma equação na outra, assim teremos uma equação só de , assim:
Vamos dividir tudo por , aí nossos termos quadráticos ficam sozinhos, e a gente consegue esboçar essa curva:
E isso é uma circunferência de raio e centro na origem. Aí o esboço dessa belezinha fica assim:
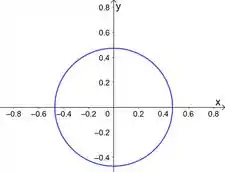
Vamos seguir!
Passo 2
b) Queremos calcular um volume de uma região entre duas superfícies. A gente pode fazer isso usando a integral tripla:
Sendo que é a região entre os parabolóides. Vamos ler as inequações que ele deu!
Isso quer dizer que nossa região está limitada por baixo pelo paraboloide . (vemos isso porque o eixo está limitado por cima pela equação do paraboloide)
E essa quer dizer que nossa região está limitada por cima pelo paraboloide .
Aí colocando num gráfico:
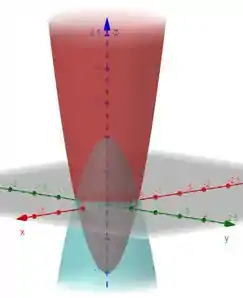
Bora ver como fazer isso!
Passo 3
A gente tem que descrever o domínio , que é essa região com formato de capsula de remédio. Percebe que a gente consegue limitar de maneira tranquila entre duas funções juntando a inequações que ele deu:
E percebe que a interseção dessas duas superfícies é uma circunferência paralela ao plano . Essas são dicas de que a gente vai usar as coordenadas cilíndricas para descrever esse domínio.
Isso significa que a gente vai aplicar as transformações:
Então para escrever os extremos de integração, limitamos essas variáveis que a gente tem: e .
Já limitamos , mas ele está entre funções de e . Precisamos aplicar nossas transformações para ele ficar entre funções de e :
Agora tá belezinha!
Passo 4
E e ? Definir elas é parecido com definir uma região em por coordenadas polares. Precisamos achar essa circunferência de interseção entre as superfícies. Mas lembra que a gente já achou isso no item (a):
A gente vê que toda nossa região (quando a gente olha para ) está contida dentro dessa circunferência. Então a gente pode dizer que:
Substituindo nossas transformações nessa inequação:
E como não há mais restrições, podemos assumir:
Belezinha?
Obs: a gente também podia limitar essas variáveis desse passo olhando o esboço da região em . Aí fica mais a seu critério mesmo.
Passo 5
Agora é montar a integral. Primeiro a gente substitui nossa transformação no nosso integrando:
Depois a gente multiplica ele por
Aí a gente pode colocar nossos extremos de integração:
Passo 6
Bora calcular essa belezura:
Prontinho!
Passo 7
c) Vamos agora calcular o centroide dessa região:
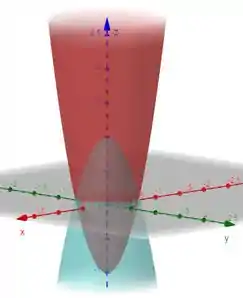
Como ela é simétrica em relação ao eixo , as coordenadas e do centroide zerão igual a zero (localização de ).
Falta a gente achar . Para isso, vamos usar a fórmulinha:
Essa integral do denominador a gente já calculou no item anterior
Então é calcular essa integral tripla aí!
Passo 8
Percebe que o domínio dela é o mesmo da integral do item (b), então a gente vai usar os mesmo extremos de integração!
Agora é montar a integral. Primeiro a gente substitui nossa transformação no nosso integrando:
Depois a gente multiplica ele por
Aí a gente pode colocar nossos extremos de integração:
Passo 9
Bora calcular essa belezura:
Aí nossa coordenada fica:
Para acabar!
Ufa! Arrasamos!
Resposta
a)
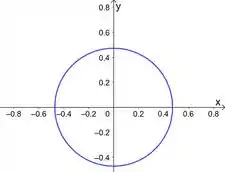
b)
c)