Seja a região limitada pelas curvas e .
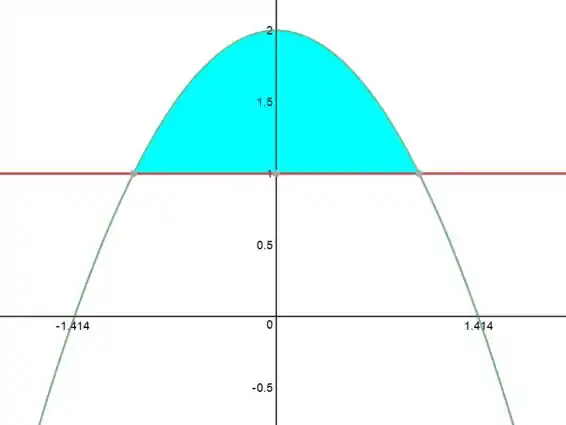
- Esboce a região .
- Encontre o volume do sólido de revolução gerado quando é girado ao redor da reta .
Passo 1
Está bem, vamos começar esboçando a região. Temos uma função , que é uma parábola côncava para baixo de raízes:
Atrelando isso a reta , temos:
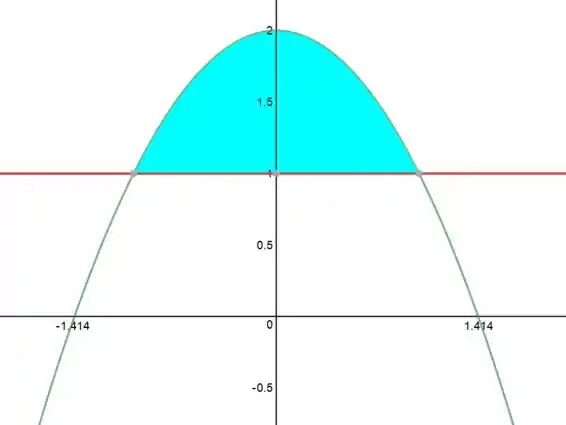
Sendo a parte entre a parábola e a reta, nossa região .
Passo 2
Queremos girar nossa região em torno da reta . Assim, usando o método dos discos cilíndricos, temos:
Onde e é a interseção. Para calcularmos os dois igualamos e :
Assim ficamos com:
Como a região é simétrica, podemos fazer:
Sendo:
Ficando:
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .