UFCG. Cálculo Diferencial e Integral II. Listas de Cálculo 2 UAMat. Lista 3. Questão 3c.
3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
(c) , .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema queremos obter o volume do solido que se forma ao rotacionar a área limitada pelas curvas e ao redor do eixo .
Esboçando as curvas e hachurando a área que é contida entre elas, vamos obter
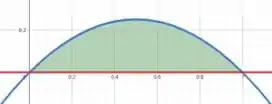
Rotacionando essa região em vamos obter um solido parecido com uma bola de futebol americano, consegue ver isso?
Mas como podemos obter o volume desse solido que é formado? 🤔
Imagine se fatiarmos o solido em infinitos pedaços cortando-o perpendicularmente ao eixo , o que vamos ter são infinitos discos de altura infinitesimal.
Essa é a ideia do método dos discos! Bora começar? 😎
Passo 2
O volume de um disco é dado por
Onde é o raio e é a altura
No caso, o raio de cada pedaço é dado pela distância de até , então em cada pedaço de volume o raio será dado por e será dado por um valor infinitesimal . Ou seja
Integrando os dois lados...
Estamos interessados apenas na região que se forma no intervalo , como vemos no esboço. Portanto aplicamos esse valor nos limites de integração de
Tirando a constante para fora da integral, vamos obter
Tranquilo até aqui? 👀
Passo 3
Vamos reorganizar a função de integração
Substituindo em
Pelo método de integração polinomial, somando no expoente de e o dividindo pelo resultado da soma.
Aplicando os limites de integração...
Substituindo esse resultado em , temos
Portanto, o volume do solido formado pela região que obtemos no passo 1, é ! Bacana, não é?
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
