Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 101123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Volume - UFRJ

Cada integral representa o volume de um sólido de revolução. Descreva a região que foi rotacionada e o eixo de rotação.

c) π ∫ 0 π / 2 [ 1 + cos ⁡ x 2 - 1 ² ] d x

Passo 1

Faaala pessoal 😊, nesse exercício vamos estudar volumes advindos de sólidos de revolução.

π ∫ 0 π / 2 1 + cos ⁡ x 2 - 1 2 d x =   ∫ 0 π / 2 [ π 1 + cos ⁡ x 2 - π 1 ² ] d x

Galerinha, a princípio lembremos que o cálculo de volume se dá integrando a função área que se prolonga ao longo de um eixo num intervalo específico. Se queremos calcular o volume gerado pela revolução da área entre duas curvas distintas, nós integramos a diferença de suas funções de área; no caso, a área da curva superior (curva cujos valores y são superiores aos da outra curva) menos a área da curva inferior.

Nesse caso, observamos uma diferença entre:

π 1 + cos ⁡ x 2   e   π 1 2

Observando que π r ² é a fórmula da área de uma circunferência, podemos entender que as curvas são:

1 + cos ⁡ x   e   1

Ou seja, queremos o volume dado pela área entre curvas, observando a integral percebemos que essa área percorre o eixo x   (estamos integrando em função de x) de zero a π 2   (nosso intervalo de integração).

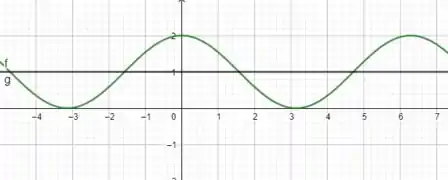
Então temos as variáveis se comportam da seguinte forma:

R = { ( x , y ) / 0 ≤ x ≤ π 2 , 1 ≤ y ≤ 1 + c o s ⁡ ( x ) }

E é isso, nos vemos por aí 😉

Resposta

c) R = { ( x , y ) / 0 ≤ x ≤ π 2 , 1 ≤ y ≤ 1 + c o s ⁡ ( x ) }

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .