Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 111123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

IME, Cálculo 1, 2021, VF, Q1B

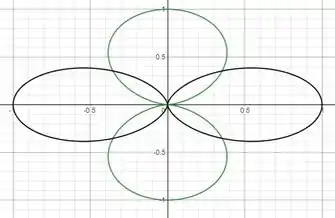
  1. Calcule o volume do sólido gerado pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais que 0 ≤ x ≤ π e sinh ⁡ x ≤ y ≤ cosh ⁡ x .
  2. Esboce no mesmo plano x y os gráficos das polares ρ 1 = sin 2 ⁡ θ e ρ 2 = cos 2 ⁡ θ , calculando a área da interseção entre elas.

Passo 1

Gaaaalera, falaí! Se liga que para esboçar gráficos polares devemos montar uma tabela ρ × θ com ângulos notáveis para que possamos determinar pontos do gráfico e depois traça-se o contorno ligando-os. Por sua vez, área em coordenadas polares é calculada através da fórmula:

A = 1 2 ∫ ρ 2 d θ

Em primeiro lugar, considere

Trace os eixos x e y e trace retas partindo da origem nos ângulos escolhidos com auxílio de régua e transferidor. Com a régua demarque as distâncias ρ 1 encontradas na direção θ correspondente e faça o traço, ligando as marcações:

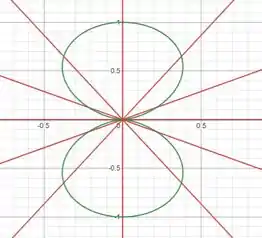
Para traçarmos ρ 2 = cos 2 ⁡ θ , seguiremos o mesmo procedimento, montando a tabela:

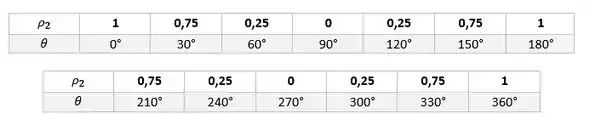
Traçando essa nova curva na cor preta usando as linhas auxiliares de antes, temos:

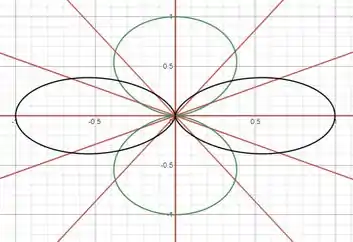
Apagando as linhas auxiliares, obtemos:

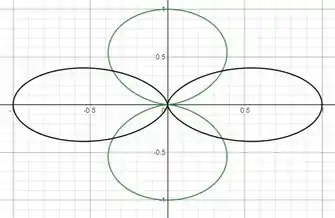
Passo 2

Observe que a interseção entre as curvas ρ 1 = sin 2 ⁡ θ e ρ 2 = cos 2 ⁡ θ se trata da origem e os ângulos θ ∈ { 45 ° ,     135 ° ,     225 ° ,     315 ° } , pois ρ 1 = ρ 2 = 1 / 2 para estes valores. Observe, contudo, que a região delimitada pela interseção pode ser dividida em 8 partes iguais a compreendida pela linha verde ρ 1 = sin 2 ⁡ θ com θ ∈ [ 0 ° ,     45 ° ] . Logo,

A = 8 1 2 ∫ 0 ° 45 ° ρ 1 2 d θ

= 4 ∫ 0 ° 45 ° sin 4 ⁡ θ d θ

Contudo, temos que para:

∫ sin n ⁡ θ d θ

Podemos utilizar:

∫ sin n ⁡ θ d θ = ∫ sin n - 2 ⁡ θ sin 2 ⁡ θ d θ

= ∫ sin n - 2 ⁡ θ ( 1 - cos 2 ⁡ θ ) d θ

= - ∫ sin n - 2 ⁡ θ cos ⁡ θ cos ⁡ θ d θ + ∫ sin n - 2 ⁡ θ d θ

E aplicando integração por partes na primeira integral:

u = cos ⁡ θ d v = sin n - 2 ⁡ θ cos ⁡ θ d θ ⇒ d u = - sin ⁡ θ d θ v = 1 n - 1 sin n - 1 ⁡ θ

Assim,

∫ sin n ⁡ θ d θ = - 1 n - 1 cos ⁡ θ sin n - 1 ⁡ θ - 1 n - 1 ∫ sin n - 1 ⁡ θ ⋅ - sin ⁡ θ d θ + ∫ sin n - 2 ⁡ θ d θ

⇒ 1 + 1 n - 1 ∫ sin n ⁡ θ d θ = - 1 n - 1 cos ⁡ θ sin n - 1 ⁡ θ + ∫ sin n - 2 ⁡ θ d θ

⇒ ∫ sin n ⁡ θ d θ = - 1 n cos ⁡ θ sin n - 1 ⁡ θ + n - 1 n ∫ sin n - 2 ⁡ θ d θ ,     n ≥ 2

Aplicando esta recorrência duas vezes, temos:

A = 4 ∫ 0 ° 45 ° sin 4 ⁡ θ d θ

= 4 - 1 4 cos ⁡ θ sin 3 ⁡ θ 0 ° 45 ° + 3 4 ∫ 0 ° 45 ° sin 2 ⁡ θ d θ

= - 1 ⋅ 1 4 + 3 ∫ 0 ° 45 ° sin 2 ⁡ θ d θ

= - 1 4 + 3 - 1 2 cos ⁡ θ sin 1 ⁡ θ 0 ° 45 ° + 1 2 ∫ 0 ° 45 ° sin 0 ⁡ θ d θ

= - 1 4 - 3 2 ⋅ 1 2 + 3 2 ∫ 0 π / 4 d θ

= - 1 + 3 2 ⋅ π 4  

= 3 π - 8 8

Resposta

A = 3 π - 8 8

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .