UFRJ, Lista 18 – Exercício 3
Calcule o volume do sólido de revolução obtido girando-se em torno do eixo a região delimitada pelo eixo , o gráfico de e as retas e .
Passo 1
E aí, galerinhaaaa! Vamos encarar mais um sólido de revolução? Pra isso, vamos desenhar as curvas para nos dá uma ideia do que vamos rotacionar.
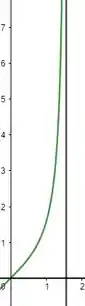
Temos que a altura da curva é dada pela própria função, ou seja,
Já a circunferência, como não iniciamos a rotação de zero, é dada por
Perceba que ai interseção ocorre em e
Sendo assim,
Passo 2
Agora vamos usar a calculadora para resolver a integral anterior, beleza ?
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .