UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 5e
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
e)
Passo 1
Oii pessoal, como vocês estão?
Pra matar mais essa questão, precisamos calcular o volume do sólido obtido pela rotação, em torno do eixo , da região delimitada pelas curvas:
Com variando no intervalo .
Eaí, alguém lembra como podemos calcular volume de sólidos de revolução?
Um método massa que é bem útil quando estamos falando de rotação em torno do eixo é o método dos discos. Segundo ele:
Então é isso! Vamos primeiro identificar a região que será rotacionada, e depois usamos o método dos discos para calcular o volume do sólido de revolução!
Passo 2
Sobre a região que será rotacionada, ela está sendo limitada pelas curvas:
no intervalo .
A primeira curva é uma função trigonométrica, o seu gráfico é do tipo:
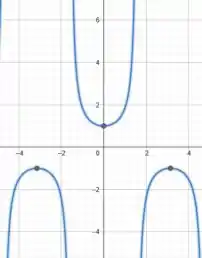
Já a segunda curva é uma função constante. Assim, colocando ambas as curvas em um mesmo gráfico e pensando no intervalo considerado, temos:
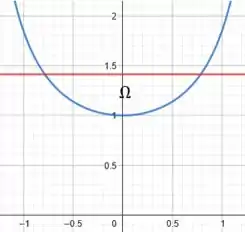
Onde as intersecções mostradas ocorrem exatamente em e . Pois:
Show de bola!
Passo 3
Agora vamos usar o método dos discos para calcular o volume obtido pela rotação desse sólido.
Como o método dos discos calcula o volume obtido pela rotação de uma região abaixo da curva . Precisaremos fazer que:
onde:
Volume obtido pela rotação da região abaixo da curva vermelha ().
Volume obtido pela rotação da região abaixo da curva azul (.
Isso no intervalo .
Como, pelo método dos discos:
Temos:
E:
Boa!
Passo 4
Show! Vamos pro nosso último passo: calcular as duas integrais.
Começando por :
Colocando as constantes para fora da integral:
Logo:
Indo agora para , vem:
Mas, lembram qual é a derivada da tangente?
Logo, pelo teorema fundamental do cálculo:
Juntando ambos os resultados na nossa equação de , vem:
Assim:
Prontinho! É isso galera, espero que vocês tenham curtido a solução. Valeeu 😊