Calcule o volume do sólido obtido pela rotação em torno do eixo , da região delimitada pelos gráficos das funções:
Passo 1
Bora lá galera, força! As funções são feias mas nem tanto! Olha só, a gente quer o volume de um sólido de revolução definido por duas funções. Essa parte em negrito que é o pulo do gato, porque se a gente tivesse funções mais amigáveis, como por exemplo:
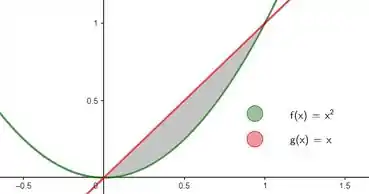
Usando o Método dos Discos, o volume seria:
Isso porque no intervalo de integração, que nada mais é do que os pontos de interseção entre e , a função está sempre por cima. Se fosse o contrário, o volume seria:
Show, então o que faremos é:
- Achar os pontos de interseção entre do nosso enunciado
- Compreender a posição relativa das funções
- Montar e calcular a integral
Partiu!
Passo 2
Pro primeiríssimo passo, podemos igualar as funções. Saca só:
Elevando os dois lados ao quadrado, temos:
Rearrumando isso, encontramos:
Limites de integração encontradíssimos! Mas e quanto as posições relativas das funções? Pra isso basta a gente fazer:
Se o resultado for exatamente nosso intervalo de integração, então fazemos tranquilamente:
Bora checar? Pra isso, temos:
O que é bem parecido com o que já fizemos anteriormente, trocando só o sinal de por um de . Como da outra vez não multiplicamos nada por , não precisamos nos preocupar com o sinal mudando de lado e virando , o que nos permite pular, já que já vimos, para:
E olha só galera! Isso aí vai ser verdade exatameeeeente para:
Que é nosso intervalo de integração! Tá feito, temos tudo pra montar a integral! O volume será:
Passo 3
Galera, agora é mão na massa, integrar, pegar o resultado, e partir pro abraço. Vamos ter como resultado:
Esses quadrados aí fizemos ambos no passo anterior, então vamos ter:
O que ainda dá pra simplificar mais e virar:
Aplicando os limites de integração, temos:
E colocando tudo no mesmo denominador:
Uhuuul, cabamos!